Квантовые явления и физика конденсированного состояния: Варианты задач по дисциплине “Физика”

Факультет материаловедения

и обработки металлов

давлением                            

Кафедра физики

КВАНТОВЫЕ ЯВЛЕНИЯ И ФИЗИКА

КОНДЕНСИРОВАННОГО СОСТОЯНИЯ

Варианты задач

По дисциплине “Физика”

Новокузнецк

2004

Министерство образования Российской Федерации

Государственное образовательное учреждение

высшего профессионального образования

 «СИБИРСКИЙ ГОСУДАРСТВЕННЫЙ ИНДУСТРИАЛЬНЫЙ

УНИВЕРСИТЕТ»

КВАНТОВЫЕ ЯВЛЕНИЯ И ФИЗИКА

КОНДЕНСИРОВАННОГО СОСТОЯНИЯ

Варианты задач

по дисциплине “Физика”

Новокузнецк

                                                   2004

УДК 536.7:519.2(07)

К60

Рецензент

Кандидат технических наук

доцент кафедры физики

металлов ГОУ ВПО «СибГИУ»

Н.Н.Кушнаренко

К60 Квантовые явления и физика конденсированного состояния. Варианты задач по дисциплине “Физика”.  / Сост.: Шарафутдинов Р.Ф., Ерилова Т.В.: ГОУ ВПО «СибГИУ».- Новокузнецк, 2004. – 36с.

Приводятся задачи для самостоятельного решения в качестве семестровых контрольных заданий (индивидуальных расчетно-графических работ). Задачи разделены по вариантам, снабжены необходимыми рисунками. Приведены основные понятия по разделам: тепловое  и рентгеновское излучение, жидкое состояние вещества и элементы кристаллографии, квантовой механики, а также  тепловые и электрические свойства твердых тел. Подбор материала ориентирован на курс физики для высших технических учебных заведений.

Работа предназначена для студентов всех специальностей.

Теоретическая часть

I. Тепловое излучение

Излучение нагретых тел называется тепловым. Первоначально были открыты и экспериментально изучены законы теплового излучения.

Закон Стефана – Больцмана: интегральная энергетическая светимость абсолютно черного тела прямо пропорциональна термодинамической  температуре в четвертой степени:

   ,

где  Е_Т   - интегральная энергетическая светимость абсолютно черного тела, т.е. энергия, излучаемая нагретым телом с единицы площади

                          Рисунок 1                                             Рисунок 2

	λ

 

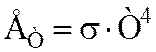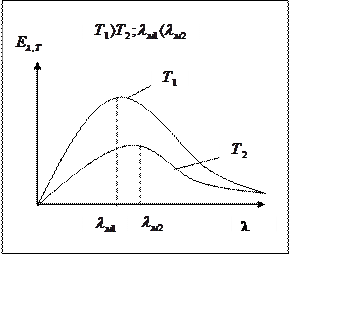
за единицу времени. (На рисунке 1 она изображается площадью под кривой   Е_{λ, Т}  от λ ).     

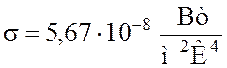   - постоянная Стефана- Больцмана, Т - термодинамическая температура.

Для серого тела энергетическая светимость равна:   , где а - поглoщательная способность серого тела.

Энергетическая светимость Е_λ связана со спектральной энергетической светимостью  абсолютно черного тела Е_{λ, Т}  соотношением:

     .

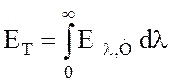где   Е_{λ, Т}  - спектральная плотность энергетической светимости –  функция распределения энергии излучения по длинам волн при определенной температуре Т. На рисунке 1 приведен вид этой функции  для абсолютно черного тела при разных температурах.

Первый закон Вина (закон смещения Вина):

Произведение длины волны соответствующей  максимальному значению спектральной плотности энергетической светимости, на термодинамическую температуру абсолютно черного тела равно постоянной величине:

,

в - постоянная в законе смещения Вина   (  ).

Второй закон Вина:

Максимальная спектральная плотность энергетической светимости абсолютно черного тела возрастает пропорционально пятой степени температуры :

   , где 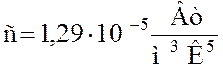       - вторая константа Вина.                           

Законы теплового излучения длительное время не находили объяснения в рамках классической физики, что получило образное название “ультрафиолетовой катастрофы”

Объяснение было дано в начале прошлого века. Планк предположил, что излучение происходит отдельными порциями энергии (квантами)   hν  , и это привело к правильному описанию законов теплового излучения

Формула Планка имеет вид:

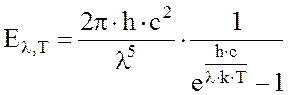
где  - спектральная плотность энергетической светимости абсолютно черного тела, λ - длина волны, с – скорость света в вакууме, k - постоянная Больцмана, Т - термодинамическая температура,  h- постоянная Планка.

II. Рентгеновское излучение

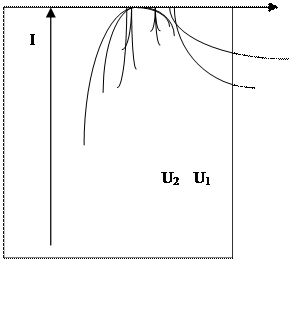
При резком торможении электронов в веществе анода, изготовленном из тяжелого металла, возникает рентгеновское излучение. Образуется спектр тормозного излучения. Он сплошной, но ограничен в области коротких длин волн (рисунок 2). Рентгеновский спектр имеет сложную структуру и зависит как от энергии электронов, так и от материала анода. Он представляет собой наложение сплошного спектра, ограниченного со стороны коротких длин волн некоторой границей λ_min , называемой границей сплошного спектра, и линейчатого спектра - совокупности отдельных линий, появляющихся на фоне сплошного спектра.

Коротковолновая граница  сплошного рентгеновского спектра находится так:

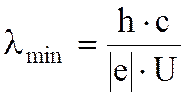  , где е = - 1,6 Кл – заряд электрона; U- ускоряющая разность потенциалов между катодом и анодом рентгеновской трубки; h- постоянная Планка.

При повышении разности потенциалов U на фоне сплошного спектра возникают пики большой интенсивности характеристического спектра. Частота (и длина волны) рентгеновских характеристических лучей может быть найдена по формуле Мозли: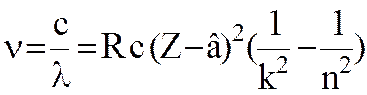

где Z- порядковый номер элемента, из которого сделан анод, в– постоянная экранирования, с - скорость света в вакууме; k и n– номера орбит,  k =1, 2, 3 , … - определяет рентгеновскую серию; n принимает целочисленные значения, начиная с (k+1) и определяет отдельную линию соответствующей серии;

R- постоянная Ридберга; она равна:          R = 1.0973    .

Закон Мозли может быть записан и так:

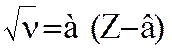 , где           .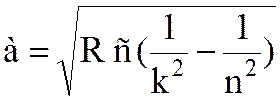

Так как   рентгеновское излучение – электромагнитные волны с малой длиной волны, то они      способны дифрагировать. Это  происходит на тонкой структуре вещества – кристаллических решетках (кристаллах). Дифракция рентгеновских лучей  описывается законом Вульфа – Брэггов:

 , где m =  1, 2… - целые числа;  d – постоянная решетки кристалла (расстояние между атомными плоскостями кристалла),

– угол между пучком рентгеновских лучей и поверхностью кристалла. Формула Вульфа – Брэггов  положена в основу структурного анализа вещества.

III.  Жидкое состояние вещества

Это агрегатное состояние вещества, промежуточное между твердым и газообразным состояниями. Поэтому ему присущи некоторые черты твердого тела (сохранять свой объем, образовывать поверхность, обладать прочностью на разрыв) и газа (сохранять