Теория построения статистических уравнений зависимостей

зависимостей являются коэффициенты сравнения факторных и результативных признаков. Способ отыскания коэффициентов сравнения определяется формой зависимостей.

Для линейных зависимостей коэффициенты сравнения  находятся путем отношения отдельных значений одноименного признака к его минимальному или максимальному уровням, служащим в качестве базы сравнения. Для параболических, гиперболических, логических и других видов зависимостей формулы для отыскания коэффициентов сравнения имеют особенный вид (они подробно будут рассмотрены позднее).

В любом случае коэффициенты сравнения показывают степень изменения (увеличения или уменьшения) величины признака по отношению к принятой базе сравнения.

Правило выбора базы сравнения для линейных зависимостей:

- при увеличении значения признака коэффициенты сравнения исчисляют от минимального уровня (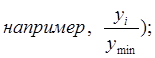

- при уменьшении значения признака коэффициенты сравнения исчисляют от максимального уровня, (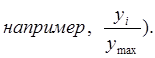

Словарь условных обозначений при работе с уравнениями зависимостей

      -    символ уравнения зависимости однофакторной связи;

символ уравнения зависимостей многофакторной связи;

минимальное и максимальное эмпирические значения результативного признака;

- эмпирические значения факторных признаков;

 - минимальные эмпирические значения факторных признаков;

 - максимальные эмпирические значения факторных признаков;

 - значения факторных признаков, соответствующие принятой базе сравнения (например, соответствующие максимальному значению результативного признака при прямой параболической зависимости, а при обратной параболической зависимости – минимальному его значению

 - символ модулей отклонений от единицы коэффициентов сравнения результативного и факторных признаков ();

- параметры уравнений зависимостей для отдельных факторных признаков (n – число факторных признаков);

B – совокупный параметр уравнения множественной зависимости;

- коэффициент корреляции однофакторной связи;

  - индекс корреляции, совместный для всех видов связи;

- размер отклонений от единицы коэффициентов сравнения теоретических значений результативного признака.

Теория и практика работы позволяют выделить следующие условия применения статистических уравнений зависимостей:

1. Сумма теоретических значений результативного признака должна равняться сумме его эмпирических значений (), т.е. сумма отклонений между эмпирическими и теоретическими значениями результативного признака равна нулю.

2. Сумма линейных отклонений теоретических значений результативного признака от их эмпирических значений должна быть минимальна, т.е. . Сравнение этих сумм позволяет установить, какой тип уравнения более подходит для характеристики изучаемого явления.

3. Сумма модулей отклонений коэффициентов сравнения эмпирических значений результативного признака от единицы () равна сумме модулей его теоретических отклонений ().

1.2. Механизм построения

статистических уравнений зависимостей

Рассмотрим случай прямой линейной однофакторной зависимости.

Проведем анализ графика теоретической прямой линейной зависимости между результативным и факторным признаками (. Коэффициенты сравнения при этом будут исчисляться от минимального уровня    Минимальное значение изучаемого признака может быть отражено на графике прямой линией, параллельной оси абсцисс. Угол между линией и теоретической линией характеризует тесноту связи между результативным и факторным признаками, а тангенс этого угла есть параметр  соответствующего статистического уравнения зависимости