Примитивно-рекурсивные и рекурсивные функции

Примитивно-рекурсивные и рекурсивные функции.

Для ученых, которых интересует лишь факт существования или не существования алгоритмов, а не сами алгоритмы, вовсе не обязательно изучать сами алгоритмы. Достаточно найти такие объекты, которые существуют или не существуют в точности тогда, когда и алгоритмы. Считают, что такими объектами являются рекурсивные функции.

Величину j называют функцией, а величины х₁, х₂, …, х_n – аргументами, или независимыми переменными, если известен закон, который для различных наборов конкретных значений величин х₁, х₂, …, х_n задает определенные значения величиныj. При этом для каждого набора допускается одно значение функции. В качестве j  может быть любой закон, но таким законом может быть и некоторый алгоритм. В этом случае функция называется вычислимой, т.к. имеется некоторый способ получить ее значение.

Функция y=j( х₁, х₂, …, х_n) называется алгоритмически вычислимой или просто вычислимой, если существует алгоритм, позволяющий определить значение функции при любых значения переменных х₁, х₂, …, х_n.

Рекурсивными функциями называется один частный класс вычислимых функций. Алгоритмы, являющиеся законами их задания называются алгоритмами, сопутствующими рекурсивным функциям.

Элементарными будем называть арифметические функции, получающиеся из неотрицательных целых чисел и переменных с помощью конечного числа сложений, арифметических вычитаний (под арифметическим вычитанием понимается абсолютная величина |x-y|), умножений, арифметических делений  (под арифметическим делением понимается целая часть частного или результат деления нацело) и построение сумм и произведений. Все элементарные функции являются вычислимыми, т.к. существуют алгоритмы для выполнения всех действий, допустимых при построении элементарных функций.

В качестве исходного числа для построения элементарных функций можно было бы взять число 1, т.к. 0=|1-1|, 2=1+1, 3= (1+1)+1 и т.д.

Примеры элементарных функций.

1)  Элементарными являются все простые функции вида j(х)ºх+1, j(у)º12у,

j(a, b, c)ºab+c, c(b)ºb² (т.к. b² = b * b) и т.д.

2) Многие из часто употребляемых функций теории чисел являются элементарными. Например:

a)  min(x, y) = ;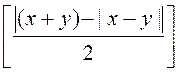

b)  sg(x) =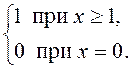

Функция sg(x) может быть выражена через функцию min(x, y): sg(x) = min(x, 1). С помощью sg(x) строится  :

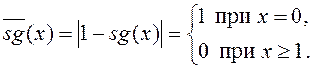
с) Неравенство x£y  эквивалентно равенству min(x, y)=х или |min(x, y)-x|=0.

Функция

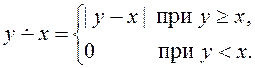
Это элементарная функция, т.к. ее можно представить в виде

d) Остаток от деления a на n

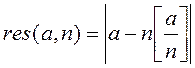
Возникает вопрос: шире ли класс всех вычислимых функций класса элементарных функций? Можно ли построить вычислимую функцию, не являющуюся элементарной?

Из всех элементарных функций быстрее всего растет произведение: an=a+a+…+a, или умножение есть итерация сложения.

Возведение в степень есть итерация умножения: 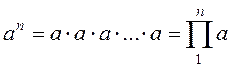. Эта функция является еще элементарной, т.к. она выражается через произведение. Растет эта функция с ростом aиn очень быстро.

Построим еще более быстро растущую функцию, являющуюся итерацией возведения в степень:

g(0, а)=а, g(1, а)=а^а, g(2, а)=

и вообще

y(n+1, а)=а^g(n,a)

Эта функция растет чрезвычайно быстро. Доказано, что с помощью построения элементарных функций уже не удается «угнаться» за ростом функции g(n, а), точнее, эта функция, начиная с некоторого а=а^* , мажорирует все элементарные функции, т.е. для любой элементарной функции j(а) найдется такое число m^*, что будет выполняться неравенство

j(а)< g(m^*, а)

для всех а ³ а^* . Но тогда легко показать, что функция g(n)=y(n, n) не является элементарной.

Действительно, если бы g(n, n)  была элементарной функцией, то нашлось бы число m^* (можно считать m^* ³ 2 в силу монотонности функции g(n, а)) такое, что g(n, n) < g(m^*, n) при n^* ³ 2. Это неравенство должно, в частности, выполняться и при n = m^*, т.к. m^* ³ 2. Получаем при этом g(m^*, m^*) < g(m^*, m^*), что невозможно.

          Т.о., итерация возведения в степень позволяет получить неэлементарную функцию. В то же время заведомо g(n, а)  вычислима при любых n = n^*, a = a^*.  Общая формула для вычисления функции g(n, а) такова g(n+1, а)=а^g(n,a)

или при a = a^*:

g(n+1, а^*)=(а^*)^g(n,a*).

Обозначим (а^*)^m= h(m); h(m) – элементарная, всюду однозначная вычислимая