3. Проектирование системы управления электроприводом
3.1 Сравнение возможных вариантов и выбор структуры СУЭП
Выбрав систему управления с поддержанием
потокосцеплением статора (![]() ) необходимо проверить,
обеспечивается ли заданная величина статизма. Проверку будем производить
использовав уравнение момента.
) необходимо проверить,
обеспечивается ли заданная величина статизма. Проверку будем производить
использовав уравнение момента.
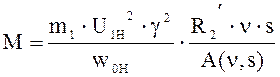 ;
;
Приняты следующие обозначения.
![]() ;
;
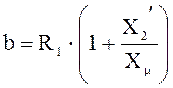 ;
; 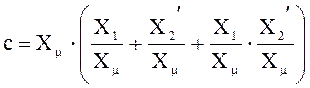 ;
;
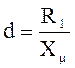 ;
; 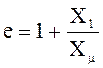 ;
;
Подставив данную зависимость в уравнение момента, получим:
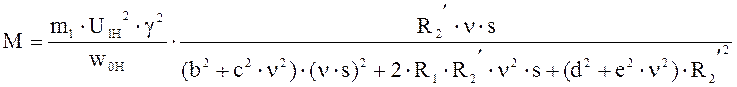
Так как:
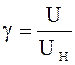 ,
а
,
а 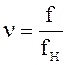 то приравняем
то приравняем ![]() .
.
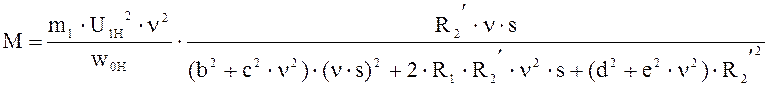
Выразим из этого уравнения значение скольжения.
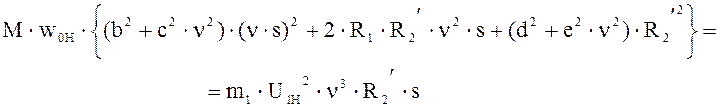
Приравняв при одинаковых степенях скольжения, получим:
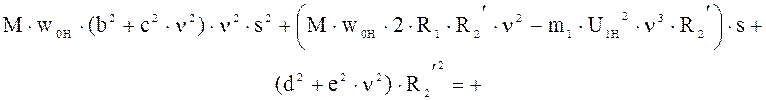 ;
;
Обозначим:
![]() ;
;
![]() ;
;
![]() ;
;
В итоге мы получили уравнение вида:
![]() ;
;
Посчитанные корни квадратного уравнения приведём в
таблицу 3.1. Видно, что данный закон управления может обеспечить величину
статизма равную ![]() , но он не обеспечивает требуемый
статизм при заданном диапазоне.
, но он не обеспечивает требуемый
статизм при заданном диапазоне.
Таблица 3.1
|
v |
D |
w |
s |
|
2 |
0,5 |
314 |
0,016 |
|
1,75 |
0,571 |
274,75 |
0,019 |
|
1,5 |
0,667 |
235,5 |
0,022 |
|
1,25 |
0,8 |
196,25 |
0,027 |
|
1 |
1 |
157 |
0,034 |
|
0,75 |
1,333 |
117,75 |
0,047 |
|
0,5 |
2 |
78,5 |
0,075 |
Для повышения величины статизма, отменим равенство ![]() , введённое выше, и введём функцию
, введённое выше, и введём функцию ![]() . Этим мы обеспечим поддержание
критического момента на максимальном уровне при изменении напряжения.
Зависимость имеет вид:
. Этим мы обеспечим поддержание
критического момента на максимальном уровне при изменении напряжения.
Зависимость имеет вид:
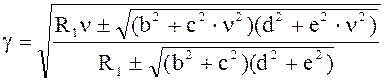 ;
;
Подставив данную зависимость в уравнение момента, и
пересчитав скольжение по той же методике, получаем значения приведенные в
таблице 3.2. Данная система управления обеспечивает статизм равный ![]() .
.
Полученное значение статизма больше чем требуемое в
задании на курсовое проектирование, но имеется возможность в процессе наладки
модели подрегулировать значение ![]() , тем самым повысить
величину статизма.
, тем самым повысить
величину статизма.
Таблица 3.2
|
v |
γ |
D |
w |
s |
|
2 |
1,913 |
0,5 |
314 |
0,018 |
|
1,75 |
1,685 |
0,571 |
274,75 |
0,021 |
|
1,5 |
1,456 |
0,667 |
235,5 |
0,024 |
|
1,25 |
1,228 |
0,8 |
196,25 |
0,028 |
|
1 |
1 |
1 |
157 |
0,034 |
|
0,75 |
0,772 |
1,333 |
117,75 |
0,044 |
|
0,5 |
0,546 |
2 |
78,5 |
0,06 |
Таким образом, выбираем закон ![]() с
поддержанием критического момента на максимальном уровне.
с
поддержанием критического момента на максимальном уровне.
3.2 Математическое описание объекта управления
Уравнения равновесия напряжения для обмоток трёх фаз статора имеют вид.
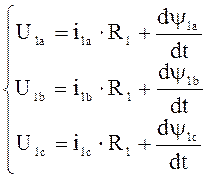 ;
;
Соответственно для обмоток трёх фаз ротора.
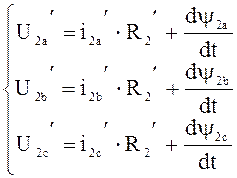 ;
;
где ![]() - мгновенные значения
фазных напряжений статора и ротора;
- мгновенные значения
фазных напряжений статора и ротора;
![]() - мгновенные значения
фазных токов статора и ротора;
- мгновенные значения
фазных токов статора и ротора;
![]() - полные
потокосцепления фазных обмоток;
- полные
потокосцепления фазных обмоток;
При математическом описании трёхфазных асинхронных электродвигателей удобно оперировать не мгновенными значениями координат, а их результирующими векторами.
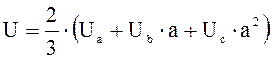 ;
;
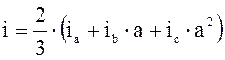 ;
;
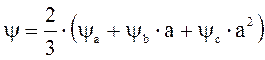 ;
;
где - ![]() ,
, ![]() ,
, ![]() ;
;
Суммируя полученные произведения, получим:
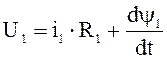 ;
;
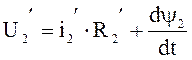 ;
;
Полученные уравнения записаны соответственно в
системах координат статора и ротора. Для совместного решения уравнений их
необходимо привести к одной системе координат. Математическое описание
процессов электромеханического преобразования энергии удобно рассматривать в
синхронных осях X и Y. ![]() .
.
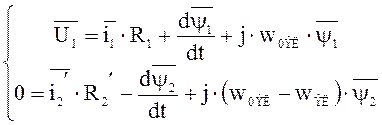 ;
;
Потокосцепления связаны с токами через индуктивности.
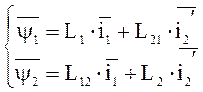 ;
;
Электромагнитный момент.
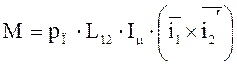 ;
;
Выразим токи через потокосцепление:
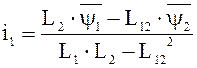 ;
;
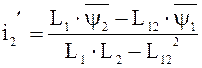 ;
;
Подставим выражения для токов в систему уравнений для напряжений. Выразим производную токов и запишем проекции уравнений на оси X и Y.
Для статора:
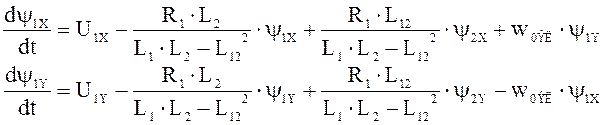 ;
;
Для ротора:
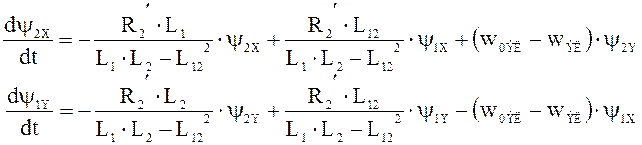 ;
;
Уравнение момента:
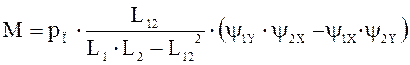 ;
;
Вид модели асинхронного двигателя в осях X и Y в системе визуального моделирования MATLAB представлен на рисунке 3.1.
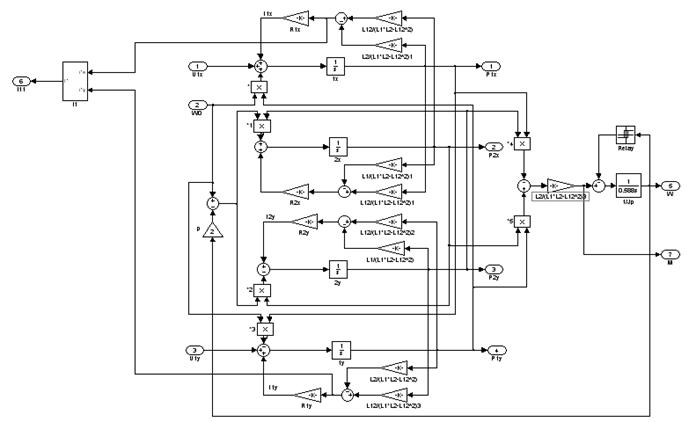
Рис. 3.1
Вид математической модели асинхронного двигателя в осях X и Y представлен на рисунке 3.2.
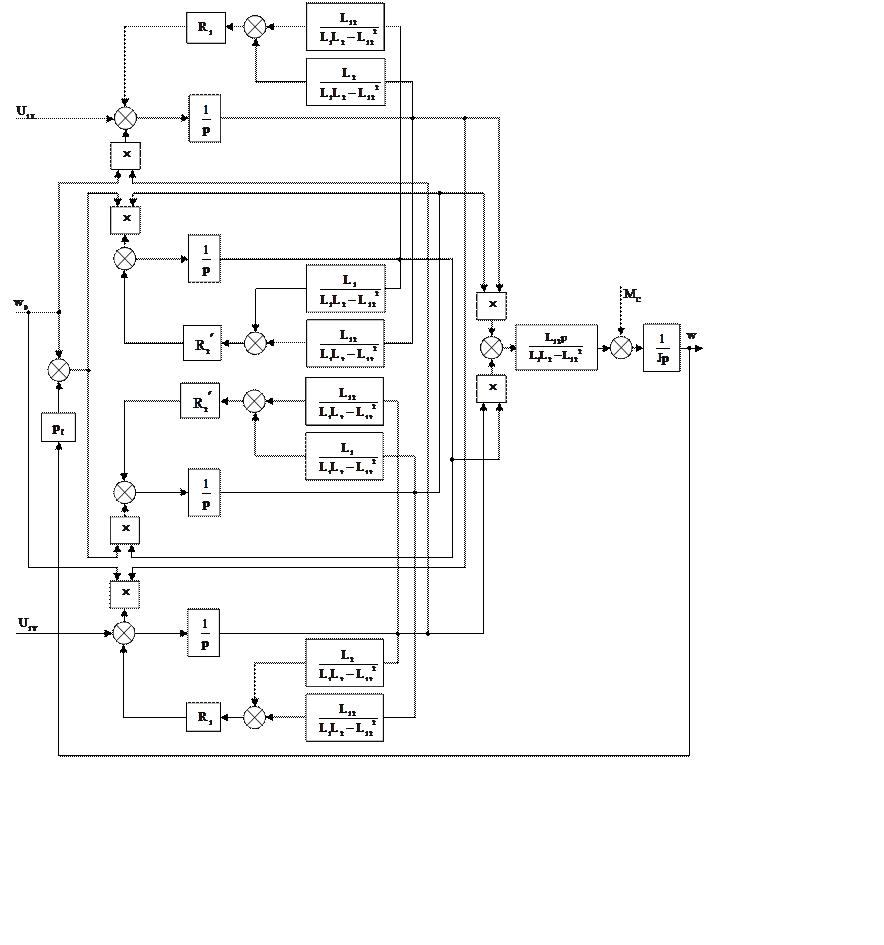
Рис. 3.2
3.3 Определение передаточных функций и коэффициентов звеньев объекта управления
При управлении электродвигателем используется обратная связь по ЭДС. ЭДС асинхронного электродвигателя определяется на основании выражения:
![]() ;
;
Коэффициент усиления схемы управления по ЭДС определяем как:
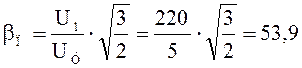 ;
;
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.