Разработка системы стабилизации частоты вращения двигателя постоянного тока с использованием оптопары, страница 3

Пропорциональный регулятор (П-регулятор).

Пропорциональный закон регулирования имеет вид:

u(t) = W_рег(p) x(t) = k₁x(t) , где k₁ – коэффициент усиления П- регулятора,

W_рег(p) – передаточная функция регулятора,

x(t) – входное воздействие.

Интегральное регулирование (И - регуляторы).

Интегральный закон регулирования имеет вид:

u(t) = k₂или u(t) = W_рег(p) x(t) = (k₂/p)x(t), где k₂ - коэффициент пропорциональности, численно равный скорости перемещения регулирующего органа при отклонении регулируемой величины на единицу ее измерения, называется коэффициентом передачи И - регулятора

Изодромное регулирование (ПИ- регулятор).

Изодромный закон регулирования имеет вид:

u(t) = k₁x(t) + k₂  или u(t) = W_рег(p) x(t) = (k₁ + k₂/p) x(t) , где k₂=1/Т_из , Т_из – постоянная времени, называемая временем интегрирования или временем  изодрома.

Регулирование с использованием производных.

Регулирование с использованием одного канала, чувствительного к производной сигнала не имеет самостоятельного значения, т.к. сигнал управления:

u(t) = W_рег(p) x(t) = k₃ p x(t) , будет равен нулю при p®0 (т.е. в установившемся режиме). Поэтому обязательно наличие параллельного либо П, либо И-канала, а чаще обоих:

u(t) = (k₁ + k₂/p + k₃ p) x(t) .

Пропорциональное регулирование с введением в закон регулирования  производной от регулируемой величины ( ПД - регулятор).

Данный закон регулирования имеет вид:

u(t) = k₁x(t) + k₃x(t)dt или u(t) = (k₁ +  k₃ p) x(t),

где k₃=1/Т_пр , Т_пр - постоянная времени   , характеризующая степень ввода в закон регулирования производной, называется постоянной времени дифференцирования, или временем предварения регулятора.

Пропорциональное регулирование с введением в закон регулирования   интеграла и производной от регулируемой величины

( ПИД - регулятор).

ПИД – закон регулирования имеет вид:

u(t) = k₁x(t) + k₃x(t)dt+k₂  или u(t) = (k₁ + k₂/p + k₃ p) x(t) .

В динамическом отношении эти регуляторы подобны системе из трех параллельно включенных звеньев: безинерционного, интегрирующего и идеального дифференцирующего.

Далее в пакете MatLab промоделируем данную систему и найдем параметры настройки ПИД–регулятора, принимая во внимания постоянные времени каждой передаточной функции. При этом отбросиваем несущественные звенья с малыми постоянными времени.  

Тогда система приобретает вид:

 

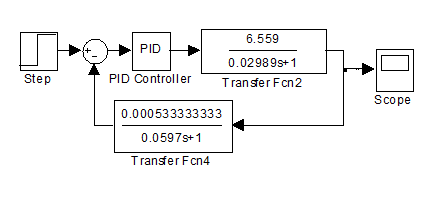
График переходного процесса приведен ниже:

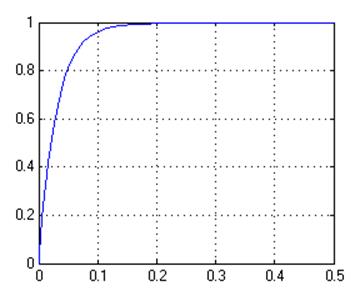
Для нахождения параметров настройки ПИД-регулятора воспользуемся пакетом MatLab:

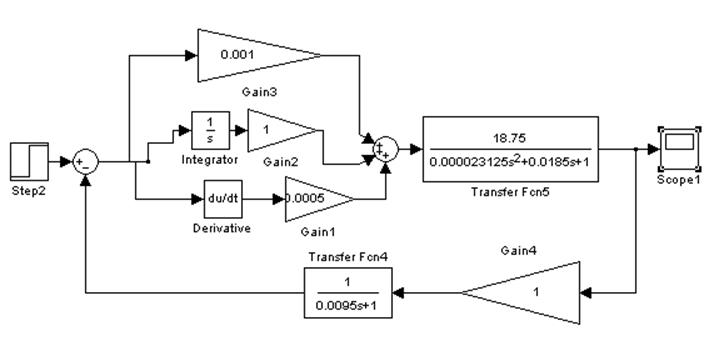
Коэффициенты ПИД – регулятора при этом равны Кр =  0,001 , Ки = 1, Кд =0,0005, отсюда находим номиналы резисторов и конденсаторов для электрической схемы ПИД – регулятора.

5. РАСЧЕТ ТОЧКИ СУММИРОВАНИЯ

Сумматор сигнала обратной связи и задающего сигнала выполним по универсальной схеме суммирования-вычитания. Схема будет иметь вид: 

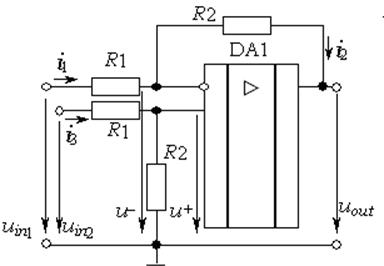
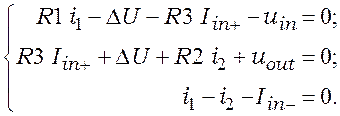
Данный ОУ  с единичным коэффициентом усиления.  R1=R2=2.2kOm

На первый вход сумматора подается сигнал с демодулятора, а на второй сигнал с задатчика. Он рассчитывается следующим образом:

Uзад=0.8Uном=0.8*12=9.6В

Т.о. на сумматоре происходит вычитание напряжения задатчика из напряжения преобразованного из частоты. На выходе сумматора имеем статическую ошибку, которую подаем на регулятор. Регулятор делает то, что уменьшает статическую ошибку.

6.Выбор структуры и расчет схемы индикации частоты вращения вала двигателя.

В цифровых устройствах для индикации параметров, текущего состояния системы и ее компонентов, результатов измерений наиболее часто применяют семисегментные индикаторы, в которых стилизованное изображение цифр составляется семью сегментами.

Свечение сегмента может происходить при подаче на него напряжения логической единицы (индикаторы с общим катодом) или напряжения логического нуля (индикатор с общим анодом).

В зависимости от того, как работает в схеме индикатор (непрерывно или периодически), различают соответственно статический и динамический типы индикации.