Методика расчета ПИ-регулятора

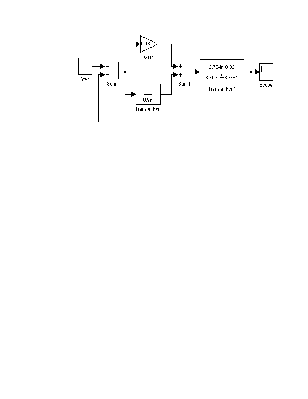
Регулятор – это устройство, выполняющие функцию поддержания выходной величины регулируемого параметра на заданном уровне. Остановим свой выбор на ПИ-регуляторе, интегральная составляющая которого исключает статическую ошибку.

АСР сушки осуществляется по двум независимым каналам: каналу регулирования влажности сушильного агента и каналу температуры сушильного агента.

Рассмотрим методику расчета ПИ-регулятора.

Передаточная функция регулятора имеет следующий вид:

Wr(p)=Кп*(1+1/Ти*p)=C1+C0/p                                                     (4.1)

Где Кп - коэффициент пропорциональности;

Ти – время изодрома.

Допустим что у нас имеются два корня характеристического уравнения Р1 и Р2, которые находятся в непосредственной близости от мнимой оси координат. Эти корни и будут определять в основном всю динамику переходного процесса Р1,2 = -a ± jb. Имея пару доминирующих комплексных корней, привяжемся к показателю колебательности y

y=1-exp(-2pm),                                                      (4.2)

где m – степень затухания, m=a/b .

Перейдем от р к jw для одного корня jw=jb. Сменим мнимую ось из начала координат в точки желаемых корней, что дает переход W( p)®W(p-h), тогда W( p) запишется следующим образом :

W(jb-a)b/b=W(j-a/b)b=W(j-m)w                                                            ( 4.3)

Выражение (4.3) является расширенной частотной характеристикой. В случаи нахождения корней на мнимой оси это будет говорить о том, что система находится на границе устойчивости.

Система находящаяся на границе устойчивости записывается в следующем виде:

Wk(j-m)w*W0(j-m)w=-1+j0                                                                   (4.4)

Тогда Wk(j-m)w=-(W0((j-m)w))                                                             (4.5)

Выделим мнимую и действительную часть Wk:

-С1-C0/((j-m)w)=mC0/((m*m+1)w) – C1+jC0/((m*m+1)w)                 (4.6)

1/(W0((j-m)w))=Im(1/(W0((j-m)w)))+Re(1/(W0((j-m)w))                     (4.7)

Преобразовав выражение, получим:

mC0/((m*m+1)w)-C1=Re(1/(W0((j-m)w))                                  (4.8)

C0/((m*m+1)w)=Im(1/(W0((j-m)w))                                           (4.9) 

Из этих выражений найдем коэффициенты С1 и С0:

С1(w)=Im((W0((j-m)w)-1)w(m*m+1)                                                     (4.10)

C0(w)=-Re((W0((j-m)w)-1)-Im((W0(j-m)w)-1)m                                   (4.11)

Рассмотрим АСР сушки по каналу температуры.

Передаточная функция регулятора АСР по каналу температуры будет иметь следующий вид:

Wt(p)=0.32*[(8.7*p+1)/(8.703*p^2+8.7*p+1)]

Отсюда следует

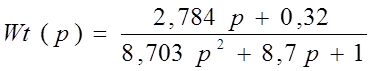
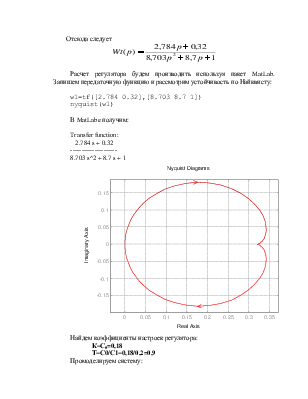
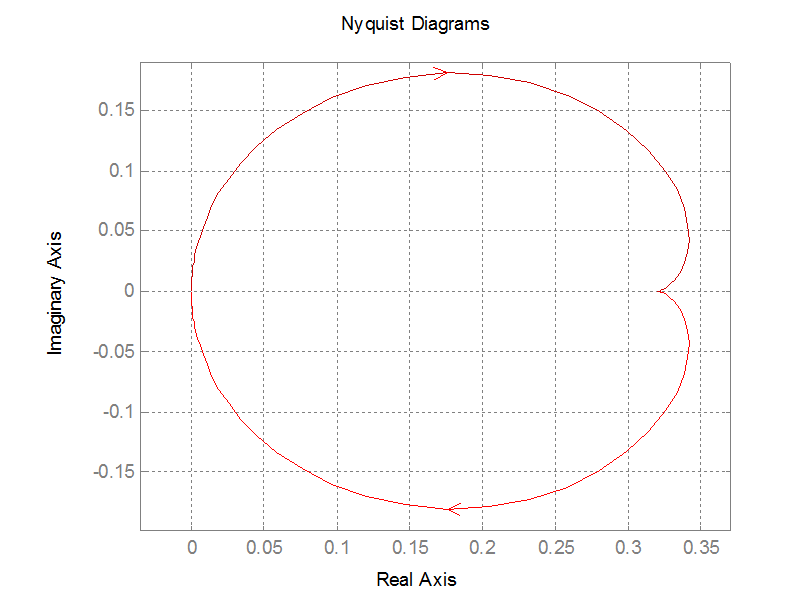
Расчет регулятора будем производить используя пакет MatLab. Запишем передаточную функцию и рассмотрим устойчивость по Найквисту:

w1=tf([2.784 0.32],[8.703 8.7 1])

nyquist(w1)

В MatLabe получим:

Transfer function:

2.784 s + 0.32

--------------------8.703 s^2 + 8.7 s + 1

Найдем коэффициенты настроек регулятора:

К=С₀=0,18

Т=С0/С1=0,18/0,2=0,9

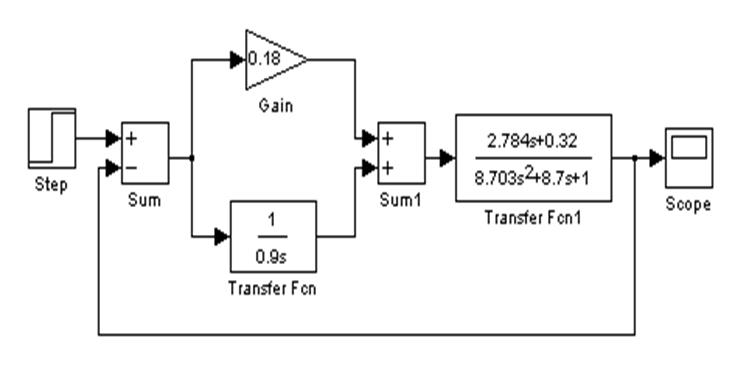
Промоделируем систему: