Динамическое программирование. Рекуррентное уравнение. Идентификация параметров передаточной функции методом площадей. Определение влажности газов

ТАУ 26-1. Динамическое программирование. Рекуррентное уравнение. Уравнение оптимальности. Проблемы исследования.

Пусть было х денег, у средств пошло на клуб, х-у на компьютер. Суммарный доход составил gy+h(x-y). Необходимо максимизировать доход. Задача оптимизации. Работаем год, потом всё продаём  a(у), полученные деньги b(х-у). Получили х₁ денег, а доход V1 распределили между собой. снова пустили в оборот. До продажи имели задачу: 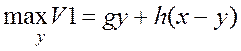. После получения прибыли . Однако задачу можно поставить сложнее. Разработаем стратегию на 2 года (прибыль за два года).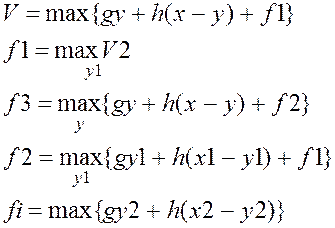

 Исходя из вычислений, получаем рекуррентное уравнение: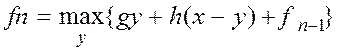 

Вывод уравнения оптимальности.

Какая бы ни была стратегия управления на предыдущих этапах, начиная с некоторого этапа, для остальных можно найти оптимальную систему управления. Исходя из этого, рассмотрим непрерывный вариант динамической системы.

Найдем экстремум. Допустим мы управляли следующим образом: обозначим .

, с момента  данный критерий принимает экстремальному значению. Разложим данное уравнение в ряд Тейлора:

.

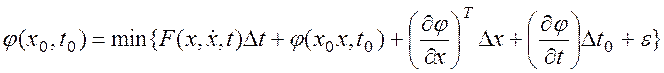Когда  и  малы, то занулим все составляющие. Тогда получим: 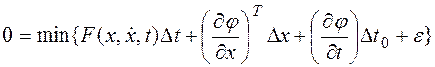 . Выразим  через  .

ТАУ 26-2

Исходя из этого имеем: 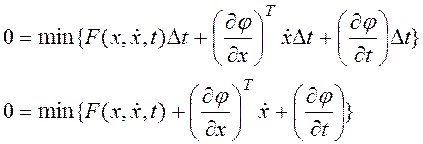. Экстремум обеспечим за счет   или . . 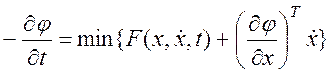Получаем уравнение для нахождения оптимального закона управления, исходя из того, что  явно не содержит ни , ни .

МОД 26-1 Идентификация параметров передаточной функции методом площадей.

Метод площадей позволяет определить передаточную функцию модели объекта по заданной графически или с помощью таблицы переходной функции h₀(t).

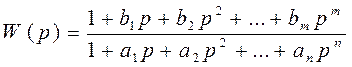, где a_i, b_i– коэффициенты передаточной функции, которые подлежат определению. Преобразуем это выражение:

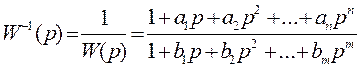. Разложим W^-1(p) в ряд Тейлора в точке р=0: 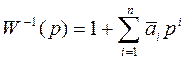, где .

Коэффициенты разложения  – площади. При известных площадях легко определяются коэффициенты передаточной функции:

.

Получим линейную систему уравнений коэффициентов  модели:

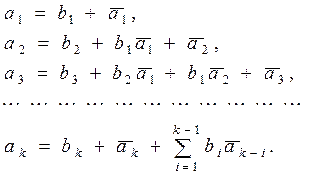
Для вычисления коэффициентов исходной передаточной функции вычисляем площадь под кривой k – h₀(t):

.

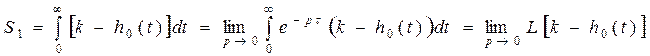Т.к. на входе - единичное воздействие, то:

, .

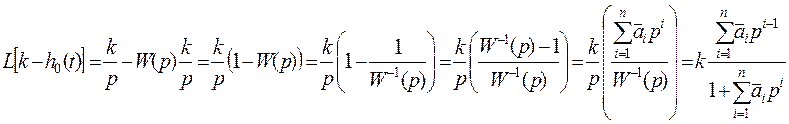
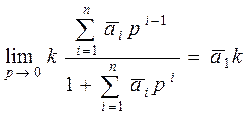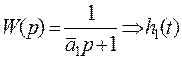Аналогично определяется S₂: . В общем случае любая i-я площадь

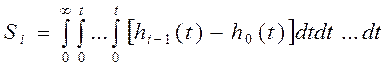. Это выражение требует многократного интегрирования, что вызывает погрешности в вычислении площадей. Поэтому применяют выражение:

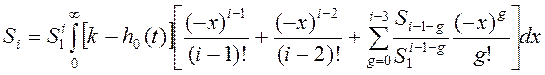 для любой площади, кроме S₁. x=t/S₁ – новая переменная. Используя эту формулу, можно найти все коэффициенты разложения W^-1(p) при n не больше 4. Разложение W^-1(p) сходится, если все

МОД 26-2

коэффициенты b равны 0. Это возможно, когда h(0)= =h’(0)=h’’(0)=0. Тогда числитель аппрок симируемой передаточной функции будет представлять собой постоянное число (коэффициент).

Порядок искомой передаточной функции определяется след. образом: если на некотором этапе расчетов S_i<<S_i-1, то порядок передаточной функции принимается равным i-1 и расчет прекращается. Если на некотором этапе расчета оказывается, что S_i<0, то порядок передаточной функции принимается равным i-1, а в числитель добавляется коэффициент b.

Достоинства метода площадей: определение коэффициентов передаточной функции можно проводить по недостаточно сглаженной переходной характеристике; метод не связан с графическими построениями; можно использовать ЭВМ. Недостатки: метод определяет коэффициенты не выше 4 порядка.

АЭП 26. Механические характеристики производственных механизмов и электродвигателей.

Силы и моменты полезной нагрузки в различных механизмах имеют различный характер. По виду их механической характеристики  () они классифицируются на типовые нагрузки.

По характеру взаимодействия с ЭП силы и моменты делят на активные и реактивные. Активные создаются внешними источниками механической энергии независимо от направления движения ЭП (подъем и спуск груза, энергия ветра и т.д.), поэтому при одном направлении они будут движущими, а при другом – тормозными.

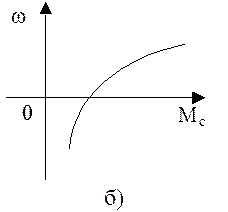
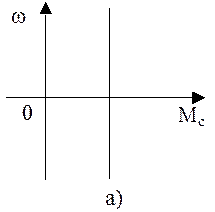Активные статические моменты:

а) постоянный по величине;

б) переменный по величине.

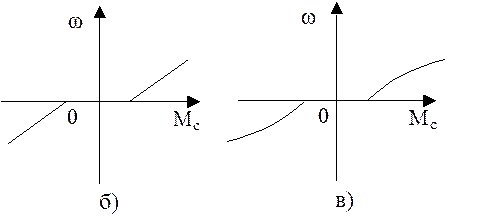
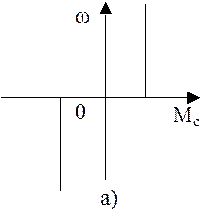Реактивные моменты препятствуют движению, т.е. всегда являются тормозными. Различают нагрузки типа «сухого» и «вязкого» трения.

Реактивные статические моменты: а) сухого трения –  Мс скачком изменяет знак при изменении направления: М=|Мс|signω;

б) вязкого трения первого рода – линейно зависят от скорости; на динамику влияют силы внутреннего вязкого терния – валов, канатов. Момент вязкого трения М=β(ω₁– ω₂), ω₁, ω₂ – скорости на входе и на выходе деформируемого элемента, β – коэффициент вязкого трения.

в) вязкого трения второго рода.

Различают нагрузки вида: М= β_мехωⁿ, β_мех – коэффициент механизма. Если n=2, то нагрузка – вентиляторная.

Статические моменты могут зависеть от пути, т.е. угла поворота ротора двигателя. Эта зависимость выражается в виде графика. Пример: механизмы подъема, напора, тяги и поворота экскаватора.

Статические моменты могут зависеть от  скорости движения и пути – электровоз, рулевое устройство корабля.

По характеру влияния на механические колебания различают моменты: консервативные – не происходит поглощения энергии колебаний системой