Синтез дискретной системы управления

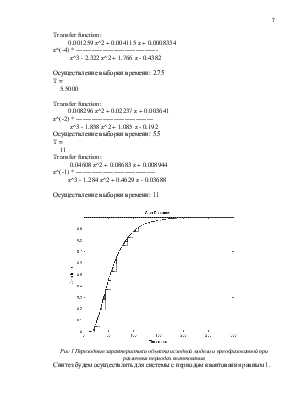
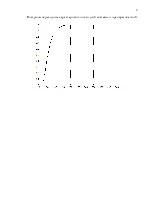
основе АКР лежит динамическое программирование и к этому добавляется некоторая функция, про которую считаем, что по своей форме она соответствует оптимальному значению критерия. Возьмем квадратичный интегральный критерий:

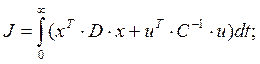
где D и C -  весовые коэффициенты матрицы, которые определяют вес переменных относительно других. Для коэффициентов можно придать различный вес. Этот выбор остается за самим проектировщиком. Матрицы D и C были выбраны в шестой главе.

Оптимальное управление:

, где  - матрица коэффициентов обратной связи по переменным x.

[k,s,e]=lqr(A,B,D,C)

k= 0.7583    0.0364    0.0066    0.2053    0.9707    0.0026    0.0006

Если в формулу для Uопт подставить, полученное ранее выражение для L, то получим:

;

Значения матрицы l являются коэффициентами обратной связи по возмущению:

l = 0.2017         0         0         0         0         0         0

Промоделируем нашу систему с учетом АКР-регулятора.

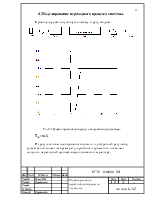
При построении оптимальной системы необходимо учесть, что разделять запаздывание на части и отделять его от объекта на практике не возможно. Для решения этой проблемы необходимо использовать дифференциаторы (реальные).

Учитывая эти моменты модель реальной оптимальной системы можно представить в следующем виде:

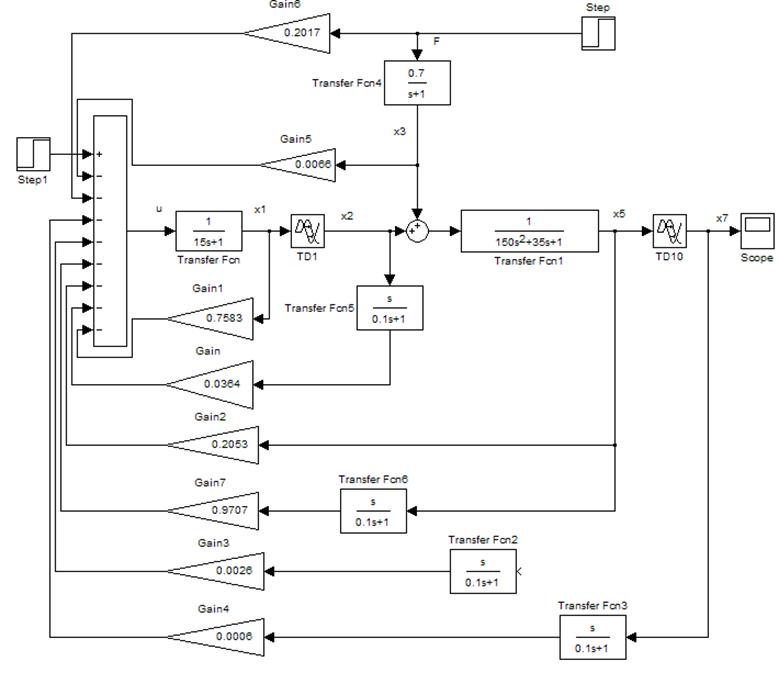
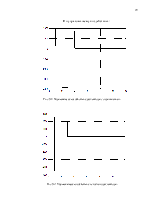
График переходного процесса будет следующим:

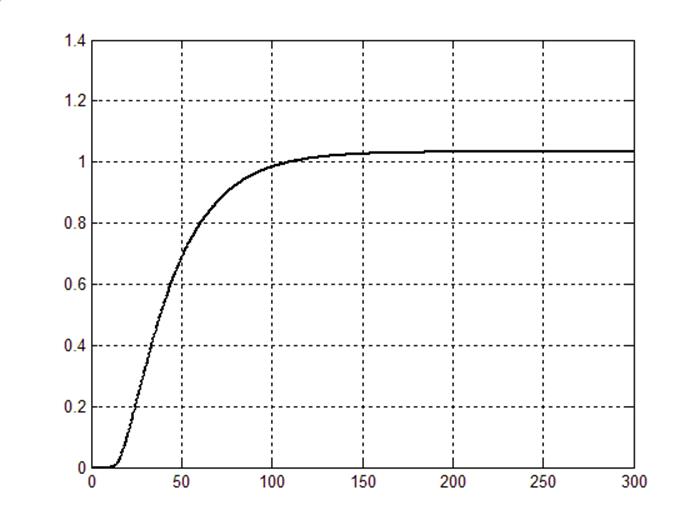
Рис 7.1 Переходный процесс АКР-регулятора.

T_пп=184.

Таким образом можно сделать вывод о том, что не имеет смысла строить систему на основе АКР- регулятора, так как система не выходит на единицу.

8. Синтез дискретного регулятора с ограничением по управлению.

Необходимо синтезировать регулятор с управлением U=0.1∙U₀ (U₀ - первоначальное управление и равно значению q0 для дискретного регулятора без ограничения по управлению).

Если увеличить время установления на один такт с  до , то можно заранее определить начальное значение управляющей переменной . Поскольку этот сигнал обычно имеет максимальную величину, его можно ограничить, задав допустимое значение   при синтезе регулятора.

Добавим еще один член в многочлены  и :

,

,

.

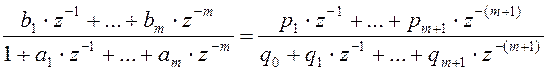Это равенство справедливо только в том случае, когда его правая часть содержит общий корень в числителе и знаменателе.

Таким образом:

.

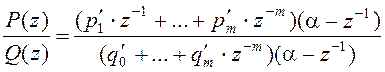После деления на  получим связь между коэффициентами  и  и коэффициентами  и .

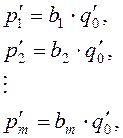
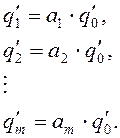
Раскрыв скобки  в предыдущем выражении, получим следующие соотношения:

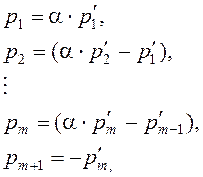
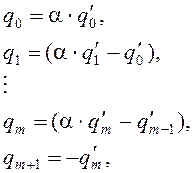
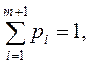
Из этих уравнений следует, что .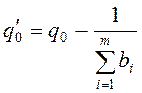

Теперь можно записать соотношения для определения параметров регулятора:

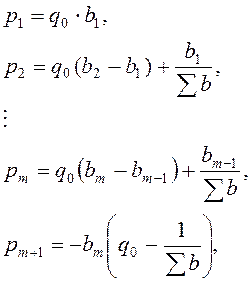
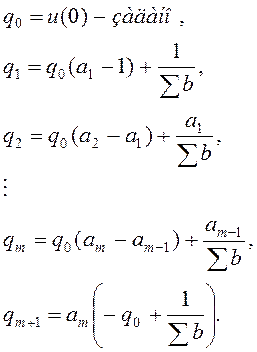
Запишем передаточную функцию регулятора:

.

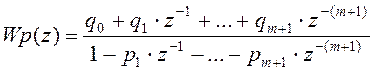В данном случае начальное значение управляющей переменной задано. Второе значение управляющей переменной будет равно:

.

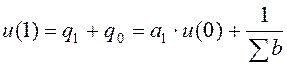Необходимо выполнения условия  т.е.:

.

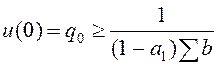Произведем расчет апериодического регулятора повышенного порядка для нашей системы. Для этого воспользуемся математическим пакетом MATLAB.

for n=2:(m-1)

v0=0.1*q0

v(1)=v0*(a1(1)-1)+(1/sum(b1))

v(n)=v0*(a1(n)-a1(n-1))+(a1(n-1)/sum(b1))

vm=a1(n-1)*(-v0+(1/sum(b1)))

x1=v0*b1(1)

x(n)=v0*(b1(n)-b1(n-1))+(b1(n-1)/sum(b1))

xm=-b1(m-1)*(v0-(1/sum(b1)))

end

V=[v0 v vm]

X=[1 -x -xm]

Wu=tf(V,X,T)

Transfer function:

260.9 z^15 + 1638 z^14 - 5748 z^13 + 5590 z^12 - 1740 z^11

---------------------------------------------------------z^15 - 0.01794 z^3 - 0.2281 z^2 - 0.615 z - 0.139

Промоделируем систему в SIMULINK’е:

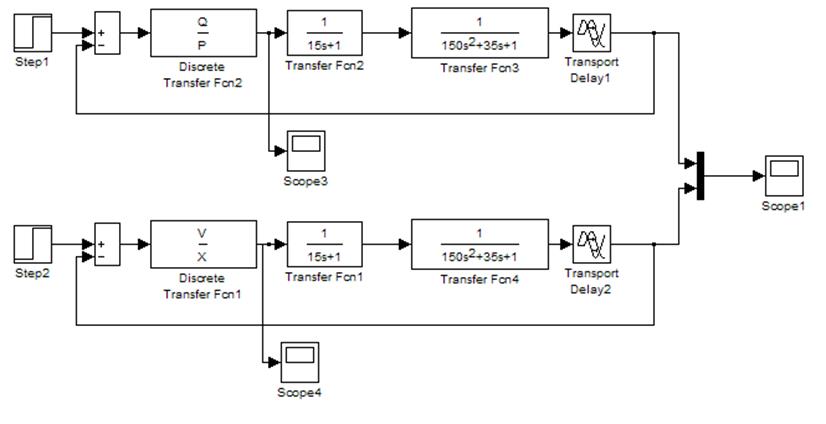
Сравним два регулятора.

По управляющему воздействию:

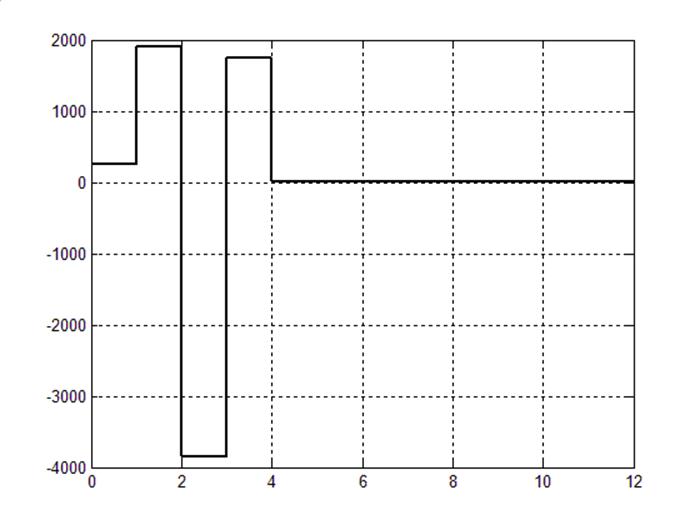
Рис.8.1. Управляющее воздействие регулятора с ограничением.

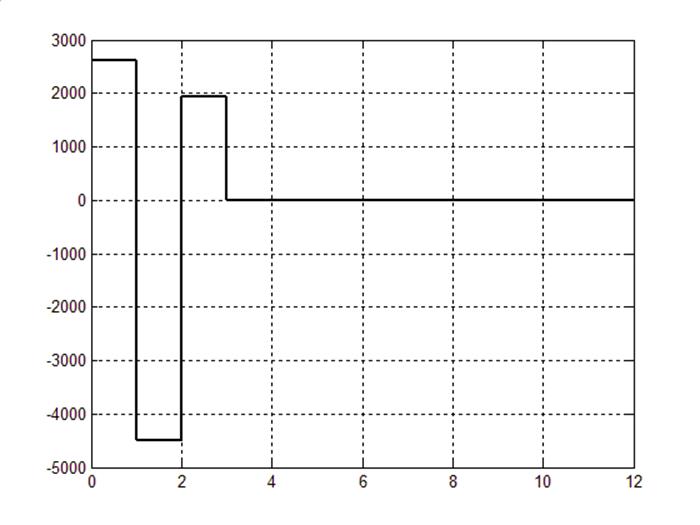
Рис.8.2. Управляющее воздействие исходного регулятора.

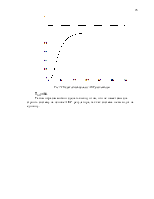
По переходному процессу:

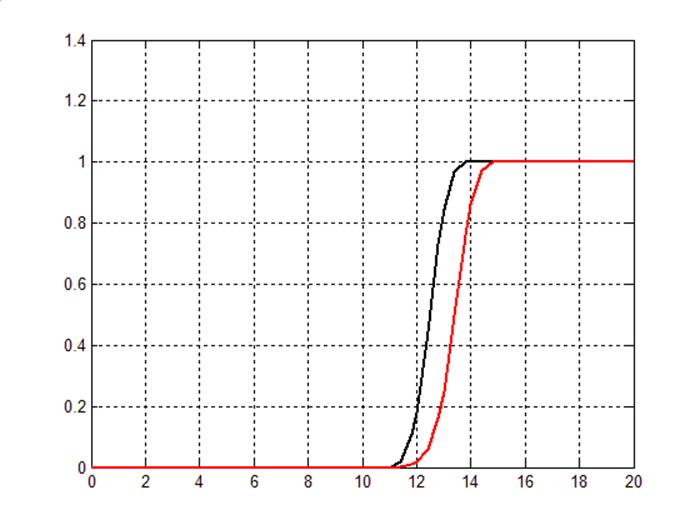
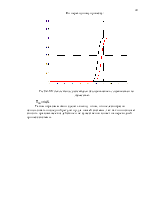
Рис.8.3. ПП для системы с регулятором без ограничения и с ограничением по управлению.

T_пп=14,5.

Таким образом можно сделать вывод  о том, что целесообразно использовать последний регулятор для нашей системы, так как он позволяет снизить правляющее воздействие и не существенно влияет на переходный процесс системы.

Заключение

В данной курсовой работе были рассмотрены основные принципы работы с дискретными системами. Так, например, были проанализированы и применены такие методы как математическое   преобразование модели объекта в дискретную модель из непрерывной, моделирование переходных характеристик объекта исходной модели и преобразованной, синтез дискретного регулятора, моделирование системы с учетом использования дискретного компенсатора, формирование критерия для оптимальной системы, аналитическое конструирование регулятора. Так же, как дополнительное задание, было выполнено ограничение по управляющему