


















W=c2d(W5,T,'ZOH') – функция c2d осуществляет перевод в дискретную область .
[a b]=tfdata(W,'a')
step(W,W5,50)Полученная передаточная дискретной модели в этом случае будет иметь вид : 2.097e-005 z^2 + 7.915e-005 z + 1.866e-005
z^(-20) * -----------------------------------------z^3 - 2.779 z^2 + 2.571 z - 0.7919
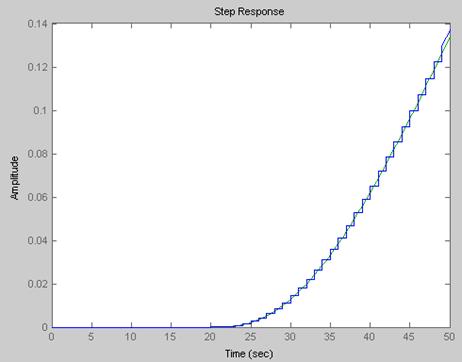
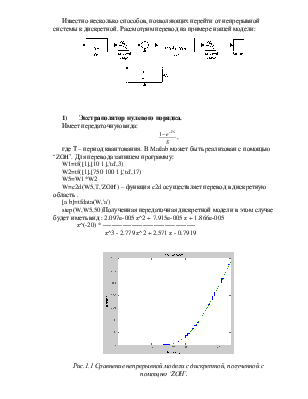
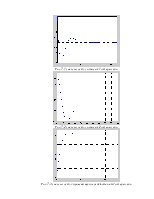
Рис.1.1 Сравнение непрерывной модели с дискретной, полученной с помощью ‘ZOH’.
2) Экстраполятор первого порядка.
Имеет вид:
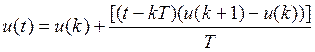
В Matlab может быть реализован с помощью ‘FOH’. Для перевода запишем программу:
T=1
W1=tf([1],[10 1],'td',3)
W2=tf([1],[750 100 1],'td',17)
W5=W1*W2
W=c2d(W5,T,'FOH')
[a b]=tfdata(W,'a')
step(W,W5,50)
Передаточная полученной дискретной модели в этом случае будет иметь вид : 5.304e-006 z^3 + 5.57e-005 z^2 + 5.316e-005 z + 4.611e-006 z^(-20) * -------------------------------------------------------------------------z^3 - 2.779 z^2 + 2.571 z - 0.7919
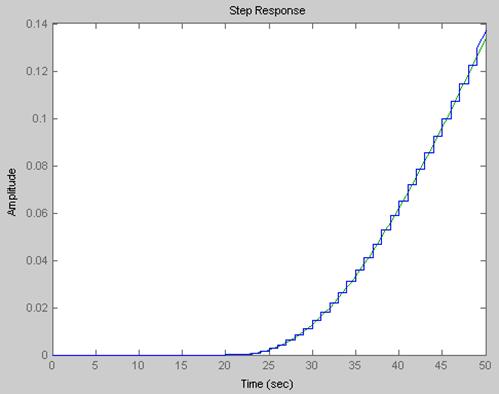
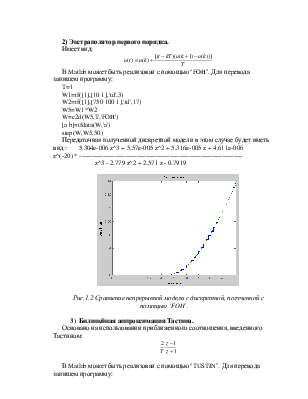
Рис.1.2 Сравнение непрерывной модели с дискретной, полученной с помощью ‘FOH’.
3) Билинейная аппроксимация Тастина.
Основано на использовании приближенного соотношения, введенного Тастином:
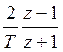
В Matlab может быть реализован с помощью ‘TUSTIN’. Для перевода запишем программу:
clc,clear
T=1
W1=tf([1],[10 1],'td',3)
W2=tf([1],[750 100 1],'td',17)
W3=c2d(W1,T,'TUSTIN')
W4=c2d(W2,T,'TUSTIN')
W5=W1*W2
W=W3*W4
[a b]=tfdata(W,'a')
step(W,W5,50)Передаточная полученной дискретной модели в этом случае будет иметь вид: 1.488e-005 z^3 + 4.463e-005 z^2 + 4.463e-005 z + 1.488e-005
z^(-20) * ----------------------------------------------------------------------------z^3 - 2.779 z^2 + 2.57 z - 0.7917
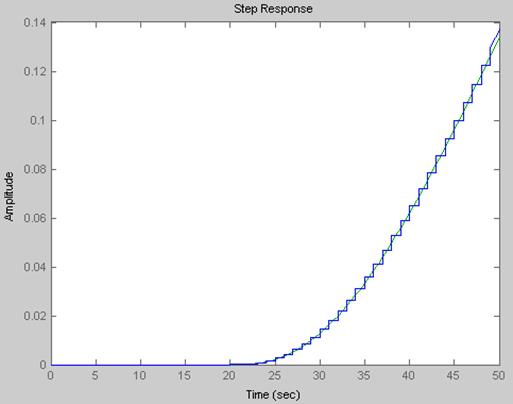
Рис.1.3 Сравнение непрерывной модели с дискретной, полученной с помощью ‘TUSTIN’.
Как видно из графиков все три способа позволяют достаточно точно перевести систему в дискретную область, хотя передаточные отличны друг от друга.
Сведем полученные коэффициенты в таблицу:
|
ZOH |
FOH |
TUSTIN |
|
|
b0 |
2,079*e-0.05 |
5,304*e-006 |
1,488*e-005 |
|
b1 |
7,915*e-005 |
5,57*e-005 |
4,463*e-005 |
|
b2 |
1,866*e-005 |
5,316*e-005 |
4,463*e-005 |
|
b3 |
0 |
4,611*e-006 |
1,488*e-005 |
|
a0 |
1 |
1 |
1 |
|
a1 |
-2.779 |
-2.779 |
-2.779 |
|
a2 |
2.571 |
2.571 |
2.571 |
|
a3 |
-0.7919 |
-0.7919 |
-0.7919 |
В дальнейшем при расчетах будем использовать экстраполятор нулевого порядка.
Теперь определим период квантования. Для этого реализуем в Matlab дискретную систему, полученную на основе непрерывной, но при различных периодах квантования.
clc,clear
T=1
W1=tf([1],[1 0.2],'td',1)
W2=tf([0.3],[35 1 0],'td',7)
W5=W1*W2
W=c2d(W5,T,'ZOH')
W6=c2d(W5,2,'ZOH')
W7=c2d(W5,7,'ZOH')
W8=c2d(W5,10,'ZOH')
[a b]=tfdata(W,'a')
step(W,W5,W6,W7,W8,50)
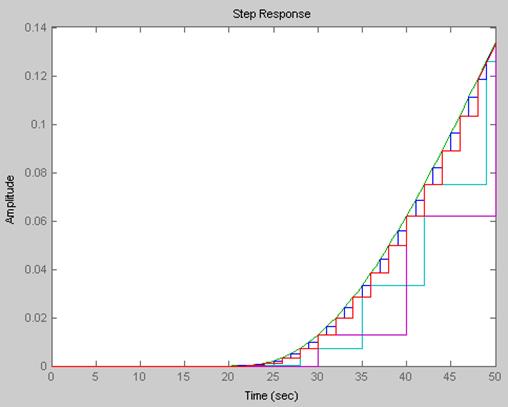
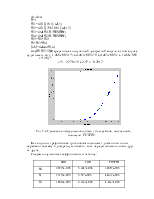
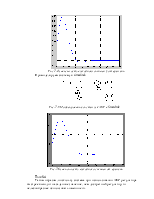
1.4. Сравнение дискретных моделей, полученных с помощью различных периодов квантования.
Из графика видно, что нет значительных отличий в полученных дискретных моделях.
В дальнейшем примем период квантования равный 1, ввиду того, что это наименьший период; полученная система достаточно точно отражает непрерывную; увеличение периода квантования не желательно, т.к. он действует на систему, как запаздывание.
На основании данных, полученных выше промоделируем систему в Simulink.
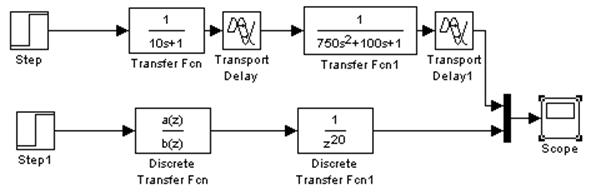
1.5 Моделирование непрерывной системы и дискретной.
Здесь 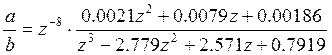
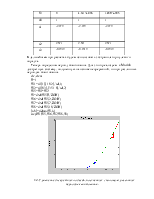
Полученная характеристика:
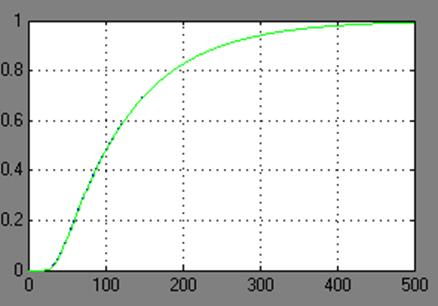
Рис.1.6. Переходные характеристики непрерывной и дискретной модели.
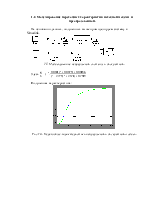
2.Построение временных и частотных характеристик объекта регулирования.
Для построения частотных характеристик в пакете MATLAB существуют определённые команды: nyquist(ww) – для построения амплитудо-фазо-частотной характеристики, и bode – для построения амплитудной и фазовой характеристик.
Построение частотных характеристик для непрерывной системы:
m-file
clc,clear,clf
ww=tf([1],[7500 1750 110 1],'td',20);
w=0:0.002:100;
nyquist(ww)
figure(2)
bode(ww)
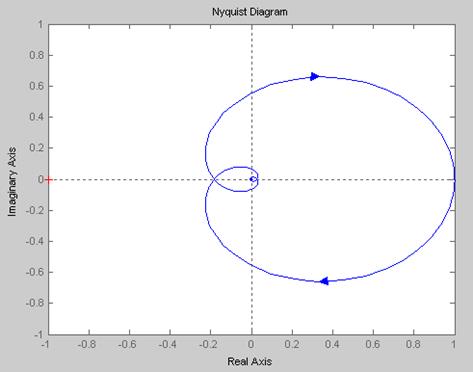
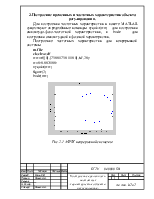
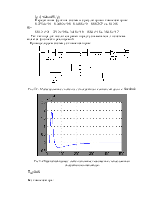
Рис.2.1 АФЧХ непрерывной системы
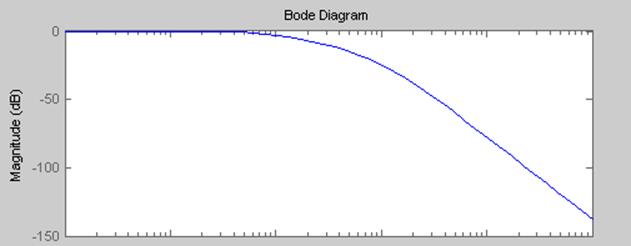
Рис.2.2 АЧХ непрерывной системы
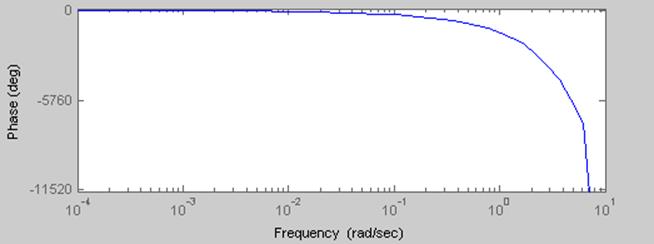
Рис.2.3 ФЧХ непрерывной системы
Для построения частотных диаграмм для дискретной системы необходимо для начала перейти в дискретную область, а затем воспользоваться известными функциями:
m-file
clc,clear,clf
ww=tf([1],[7500 1750 110 1],'td',20);
wwww=c2d(ww,30)
nyquist(wwww)
figure(2)
bode(wwww)
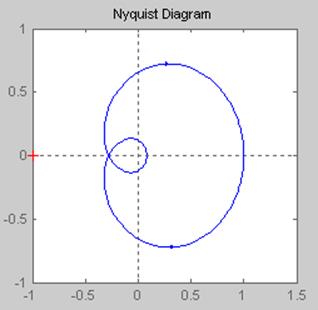
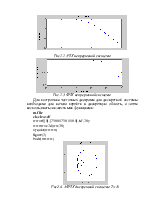
Рис2.4. АФЧХ дискретной системы T=10
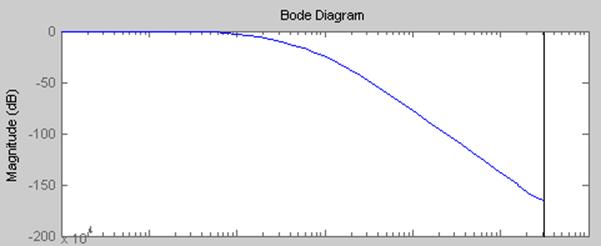
Рис.2.5 АЧХ дискретной системы T=10
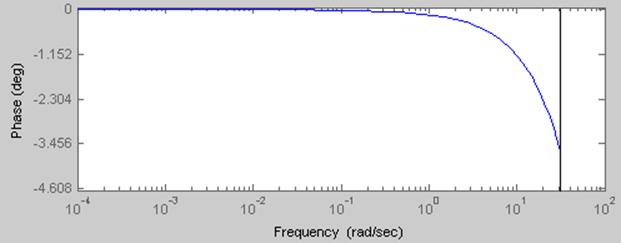
Рис.2.6 ФЧХ дискретной системы T=10
Для построения временных характеристик воспользуемся командой step(ww) (реакция системы на единичное воздействие):
m-file
clc, clear
ww=tf([1],[7500 1750 110 1],'td',20);
step(ww)
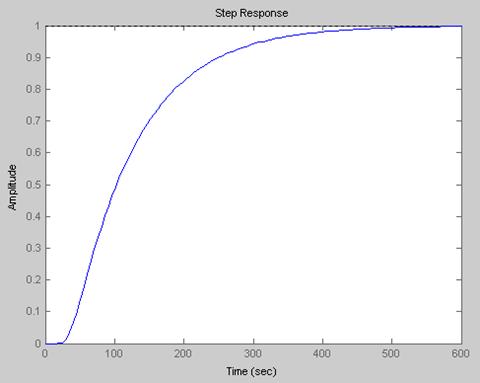
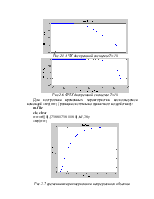
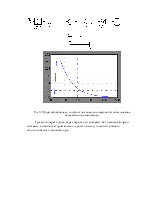
Рис.2.7 временная характеристика непрерывного объекта
Для дискретного объекта, алогично с предыдущим случаем, переведём систему в дискретный вид, а затем уже строим реакцию объекта на единичное воздействие:
m-file
clc, clear
ww=tf([1],[7500 1750 110 1],'td',20);
www=c2d(ww,10,'ZOH')
step(www)
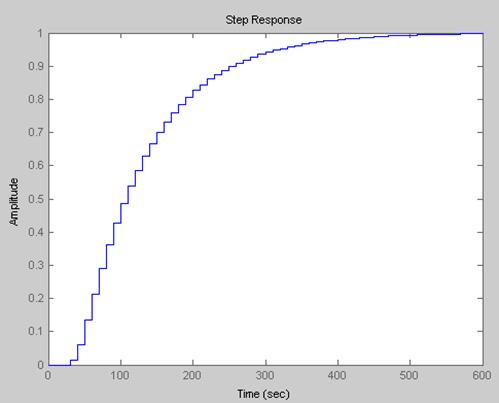
Рис.2.8 временная характеристика для дискретной системы
3. Синтез дискретного регулятора.
Для синтеза нужно знать качественные показатели, необходимо на основе существующих систем знать требования к структуре регулятора. Будем считать, что технологический объект представляет собой непрерывное динамическое звено. Для технологических процессов практически не используется вариант параллельного включения регулятора. Поэтому будем рассчитывать регулятор, включенный последовательно с объектом.
Для системы вида:

требуется рассчитать дискретный регулятор.
При расчете данного регулятора принимают следующие положения:
- за n тактов переходной процесс завершается (tрег=mT);
- переходный процесс близкий к апериодическому.
Эти условия сложно обеспечить типовыми законами регулирования, следовательно, этот регулятор имеет более сложную структуру.
Пусть передаточная объекта имеет вид:
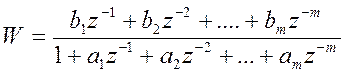
Тогда передаточная дискретного регулятора будет иметь вид:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.