Численные методы моделирования уравнений в частных производных

Лабораторная работа 1.

Численные методы моделирования уравнений в частных производных.

Постановка задачи: уравнение диффузии.

Где с-концентрация (с - пространственная переменная,t – переменная времени ).

Граничные условия:

Если х=0, то

Если х=L, то c(L,t)=f2(t)

Начальные условия:

1)  Метод сеток

Апроксимация производных в точках разбиения в матричном виде.

Подставим обе части в исходное уравнение и выразим c(I,j+1):

Обозначим:  – критерий (задается в пределах [0,0.5] возьмем А=1/3).

Задаем граничные условия:

Пишем программу:

clc, clear

t(1)=0

x(1)=0

m=200

n=10

dt=0.1

dx=0.1

for j=1:m

    f1(j)=10+5*exp(-0.1*t(j));

    f2(j)=10+5*cos(t(j));

    t(j+1)=t(j)+dt;

end

for i=1:n

    f3(i)=15+sin(x(i));                                    

    x(i+1)=x(i)+dx;

end

C(1,1:m)=f1;

C(n,1:m)=f2;

C(1:n,1)=f3';

A=1/3

for j=1:m-1

    for i=2:n-1

        C(i,j+1)=(1-2*A)*C(i,j)+A*(C(i+1,j)+C(i-1,j));

    end

end

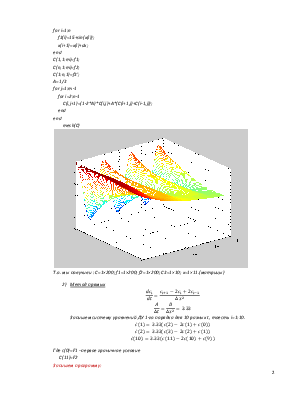
        mesh(C)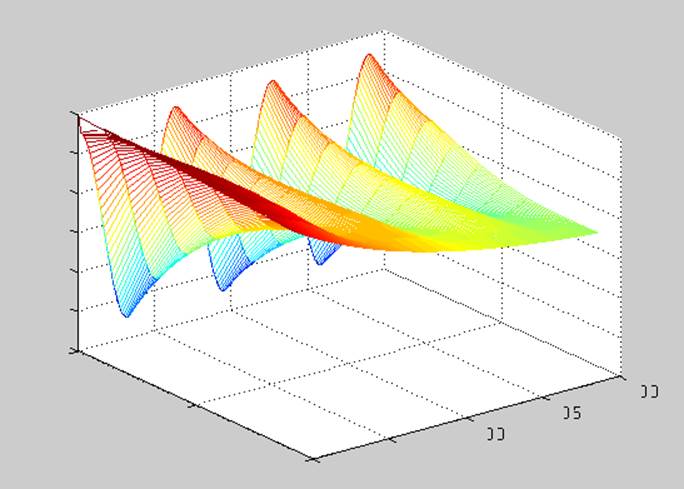        

Т.о. мы получили : С=1×200; f1=1×200; f2=1×200; C3=1×10; x=1×11.(матрицы)

2)  Метод прямых

Запишем систему уравнений ДУ 1-го порядка для 10 разных t, тоесть i=1:10.

Где с(0)=F1 –первое граничное условие

     С(11)=F2

Запишем программу:

funktion u=tb(t,c)

u=[3.33*(c(2)-2*c(1)+(10+5*exp(-0.1*t)));

   3.33*(c(3)-2*c(2)+c(1));

   3.33*(c(4)-2*c(3)+c(2));

   3.33*(c(5)-2*c(4)+c(3));

   3.33*(c(6)-2*c(5)+c(4));

   3.33*(c(7)-2*c(6)+c(5));

   3.33*(c(8)-2*c(7)+c(6));

   3.33*(c(9)-2*c(8)+c(7));

   3.33*(c(10)-2*c(9)+c(8));

3.33*((10+5*cos(t))-2*c(10)+c(9))];

tn=0

tk=10

x(1)=0

dx=0.1

n=10

for i=1:n

                  f3(i)=15+sin(x(i));

                 x(i+1)=x(i)+dx;

end

[T C]=ode45('tb',[tn tk], f3)

mesh(C)