Исследование устойчивости системы стабилизации угла рыскания ЛА с помощью критериев и моделирования

Балтийский государственный

технический университет

им. Д. Ф. Устинова

«ВОЕНМЕХ»

Кафедра А5

Лабораторная работа по ТАУ №4

«Исследование устойчивости САУ. Построение области устойчивости в плоскости передаточных чисел автопилота i₁ и i₂»

Вариант №18

	Выполнил: Шерин П. А. ст. гр. А481 Проверил: Санников В. А.

 

Санкт-Петербург 2012 год

Содержание лабораторной работы.

Цель лабораторной работы………………………………………………….стр. 2

Описание лабораторной работы……………………………………………стр. 2

Исходные данные к лабораторной работе…………………………………стр. 4

Исследование устойчивости САУ …………………………………………. стр.4

Листинг программы ………………………………………………………... стр. 4

Построение области устойчивости в плоскости передаточных чисел автопилота i₁ и i₂ ……………………………………………………………. стр.7

Листинг программы …………………………………………………………стр. 7

Определение области устойчивости САУ ………………………………..стр. 10

Цель работы: исследование устойчивости системы стабилизации угла рыскания ЛА с помощью критериев и моделирования. С помощью метода D – разбиения и моделирования построение области устойчивости и плоскости передаточных чисел i₁ и i₂ автопилота.

Описание лабораторной работы.

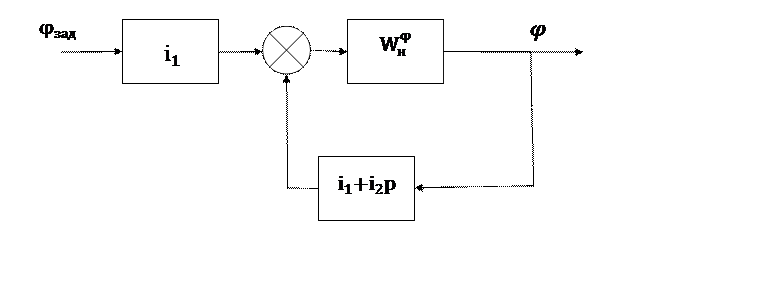
Рассмотрим систему стабилизации углового движения ЛА относительно ц. м. в горизонтальной плоскости. В качестве программного движения принимаем полет ЛА на заданной высоте с постоянной скоростью. Принимается, что динамика системы стабилизации угла рыскания описывается линейными дифференциальными уравнениями в отклонениях относительно программного движения:

(1)

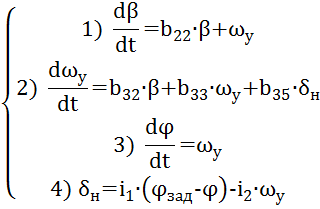
В данной системе уравнений (1) введены следующие обозначения: β – угол скольжения, δ_н – угол отклонения руля направления, φ – угол рыскания, ω_y – угловая скорость рыскания, b_ij – известные динамические коэффициенты, i₁, i₂ – передаточные числа, φ_зад – известная функция, задающая программу угла рыскания. Уравнения 1)-3) описывают динамику ЛА, уравнение 4) – уравнение системы управления. При этом рулевая машинка считается безынерционной.

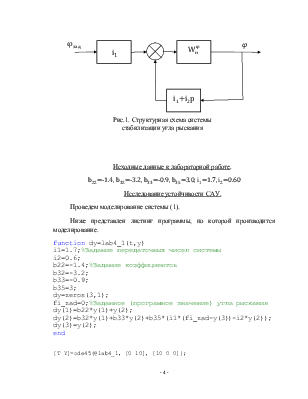
Системе уравнений (1) соответствует структурная схема системы стабилизации угла рыскания, приведенная на рис. 1.

Рис.1. Структурная схема системы стабилизации угла рыскания

Исходные данные к лабораторной работе.

Исследование устойчивости САУ.

Проведем моделирование системы (1).

Ниже представлен листинг программы, по которой производится моделирование.

function dy=lab4_1(t,y)

i1=1.7;%Задание передаточных чисел системы

i2=0.6;

b22=-1.4;%Задание коэффициентов

b32=-3.2;

b33=-0.9;

b35=3;

dy=zeros(3,1);

fi_zad=0;%Заданное (програмное значение) угла рыскания

dy(1)=b22*y(1)+y(2);

dy(2)=b32*y(1)+b33*y(2)+b35*(i1*(fi_zad-y(3))-i2*y(2));

dy(3)=y(2);

end

[T Y]=ode45(@lab4_1, [0 10], [10 0 0]);

figure;

plot(T, Y(:,1));

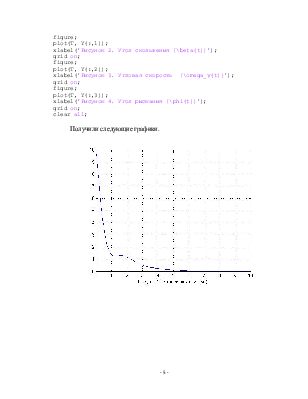
xlabel('Рисунок 2. Угол скольжения {\beta(t)}');

grid on;

figure;

plot(T, Y(:,2));

xlabel('Рисунок 3. Угловая скорость  {\omega_y(t)}');

grid on;

figure;

plot(T, Y(:,3));

xlabel('Рисунок 4. Угол рыскания {\phi(t)}');

grid on;

clear all;

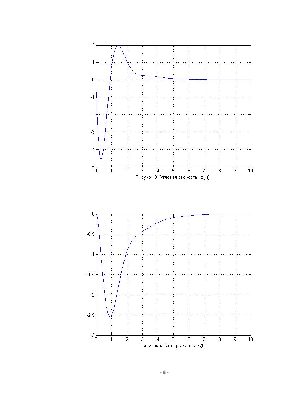
Получили следующие графики.

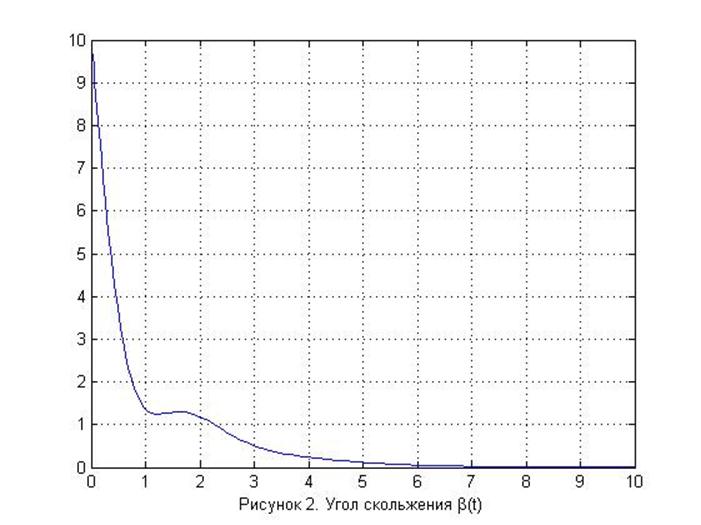
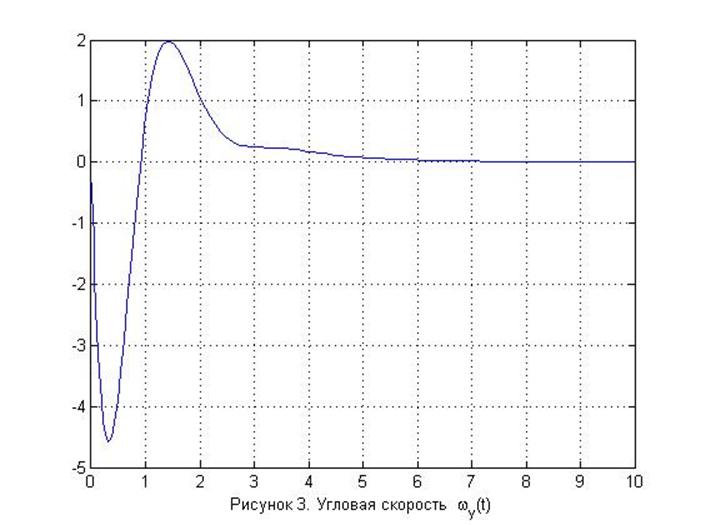
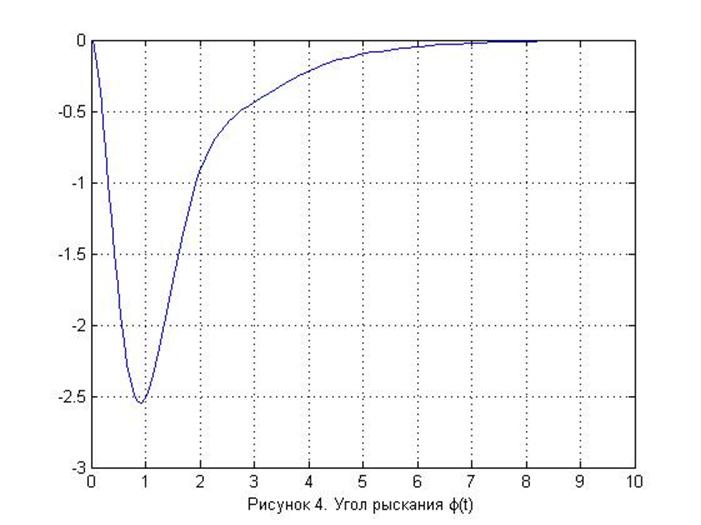
Из выше представленных графиков видно, что за время переходного процесса параметры β(t), ω_y(t), φ(t) – затухающие, следовательно, САУ устойчива. 

Построение области устойчивости в плоскости передаточных чисел автопилота i₁ и i₂.

Имеем характеристическое уравнение системы стабилизации угла рыскания:

Уравнение особой прямой определяется соотношением i₁=0.

Для построения границ устойчивости в уравнение (2) поставляется p=j·ω. Получаем:

Приравнивая вещественную и мнимую часть в уравнении (3), получим два уравнения для определения i₁ и i₂:

-b₃₅·b₂₂·i₂-b­₃₅·ω²·i­₂=-(b₂₂+b₃₅)·ω²;

b₃₅·ω·i₁-b­₃₅·b­₂₂·ω·i­₂=ω³-ω·b₂₂b₃₃+ω·b₃₂. (4)

Решение системы (4) имеет вид:

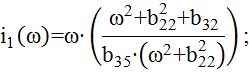
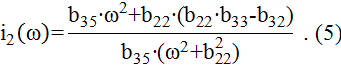
Для автоматического определения i₁(ω) и i₂(ω) составим программу.

Ниже будет приведен листинг программы на языке программирования Matlab. В “%” будут приведены комментарии к соответствующим блокам программы.

clear all;

global ii1;

global ii2;

b22=-1.4;

b32=-3.2;

b33=-0.9;

b35=3;

w=0;

i=1;

i1(i)=w^2*(w^2+b22^2+b32)/(b35*(w^2+b22^2));%Выражение для вычисления i1(w)

    i2(i)=(b33*w^2+b22*(b22*b33-b32))/(b35*(w^2+b22^2));

    i=i+1;

    w=w+0.1;

grid on;

figure;

plot(i1,i2,'-');

xlim([-1 5]);

ylim([-3 3]);

line([0 0],[-5 5]);

grid on;

xlabel('i1');

ylabel('i2');

hold on;

ii1=1.7;

ii2=0.6;

title('Область D-разбиения');

plot(ii1,ii2,'x');

plot(ii1,-ii2,'x');

Далее получаем графики.

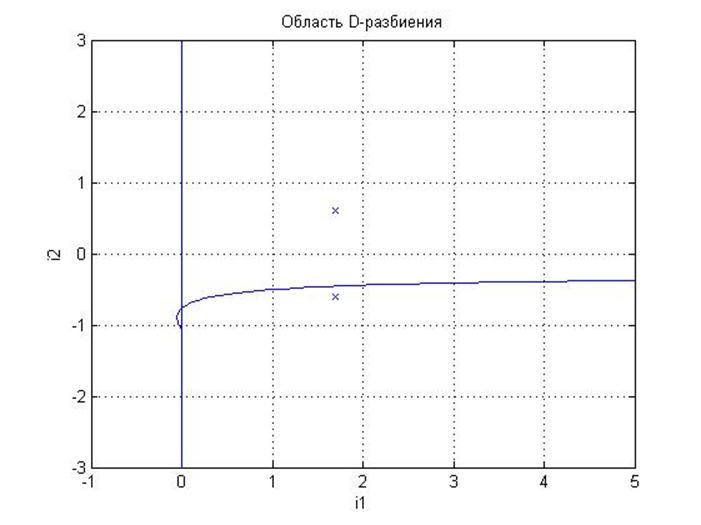
Определим область устойчивости САУ. Для этого из каждой полуплоскости передаточных чисел i₁ – i₂ выберем по одной точке. Если условие устойчивости будет выполняться для этой точки, следовательно, будет выполняться и для всей области.

Исследование устойчивости проведем по критерию Гурвица.

Из верхней полуплоскости выберем произвольную точку с координатами i₁=3, i₂=2.

Далее определяем коэффициенты a_j для уравнения (2):

a₀=1;

a₁=-(b₂₂+b₃₃-b₃₅·i₂)=-(-1,4-0,9-3·2)=8,3;

a₂=b₂₂·b₃₃-b₃₂+b₃₅·i₁-b₃₅·b₂₂·i₂=1,26+3,2+9+3·1,4·2=16,26;

a₃=-b₃₅·b₂₂·i₁=12,6;

Составляем определитель матрицы Гурвица:

 

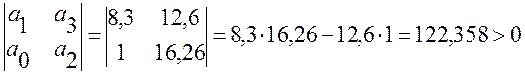
Следовательно, САУ устойчива.

Проверим устойчивость САУ для точки i₁=3, i₂=-2.

a₀=1; a₁=-3,7; a₂=5,06; a₃=12,6.

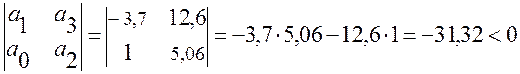
Условие устойчивости САУ не выполнено.

Следовательно, область устойчивости находится выше D- кривой (см. рисунок 6).