Аналитическая группировка по размеру прибыли банков. Построение графика зависимости между численностью сотрудников и размером прибыли

Министерство образования и науки Российской Федерации

Федеральное государственное бюджетное образовательное

учреждение высшего профессионального образования

«Комсомольский-на-Амуре государственный

технический университет»

Факультет экономики и менеджмента

Кафедра «Экономика и финансы»

РАСЧЁТНО-ГРАФИЧЕСКОЕ ЗАДАНИЕ

по дисциплине «Статистика»

Студент группы 0ФК-2                                                 И. П. Тарасенко

Преподаватель                                                                И. И. Антонова

2011

Задача №8 По данным таблицы 1 произведите аналитическую группировку по размеру прибыли банков. Постройте график зависимости между численностью сотрудников и размером прибыли. Произведите анализ полученных результатов.

Таблица 1 – Данные по 20-ти коммерческим банкам региона за год

Номер банка	Число сотрудников	Прибыль, млрд.р.	Номер банка	Число сотрудников	Прибыль, млрд.р.
1	1015	28,6	11	3030	103,5
2	2995	130,2	12	515	15,5
3	2150	28,5	13	705	38,5
4	265	32,2	14	1750	53,8
5	3738	151,5	15	2675	27,5
6	430	11,9	16	130	13,9
7	1920	109,0	17	1615	37,4
8	315	35,6	18	1220	33,1
9	200	20,0	19	1370	42,5
10	2100	92,3	20	1580	57,2

Решение:

1. В качестве факторного (группировочного) признака примем прибыль банков, а результативного количество сотрудников. Образуем пять группы банков с разными интервалами.

R = Хmах – Хmin,                                     (1)

R = 151, 5-11, 9 =139, 2 млрд. руб.

Выберем количество групп в зависимости от объема статистической совокупности. Так как объем совокупности, т.е. число предприятий равно 20, то количество групп, т. е. n = 5.

Рассчитаем величину равного интервала по следующей формуле:

h = R / n,                                                 (2)

h = 139,2 / 5 = 27,92 млрд. руб.

Таким образом, получаем следующие группы:

1 группа 11,9 – 39,82 млрд. руб.

2 группа 39,82 – 67,74 млрд. руб.

3 группа 67,74 – 95,66 млрд. руб.

4 группа 95,66 – 123,58 млрд. руб.

5 группа 123,58 – 151,5 млрд. руб.

Все вычисления будем вносить в таблицу 2:

Группы банков по количеству прибыли	Число банков	Прибыль, млрд. руб.		Число сотрудников, чел.
		всего	в среднем на 1 банк	Всего	в среднем на 1 банк
11,9 – 39,82	12	322,70	26,89	11226,00	935,50
39,82 – 67,74	3	153,50	51,17	4700,00	1566,67
67,74 – 95,66	1	92,30	92,30	2100,00	2100,00
95,66 – 123,58	2	212,50	106,25	4950,00	2475,00
123,58 – 151,5	2	281,70	140,85	6733,00	3366,50
ИТОГО	20	1062,70	417,46	29709,00	10443,67

По данным таблицы 2 видим, что наибольшую прибыль получают банки с наибольшим числом сотрудников.

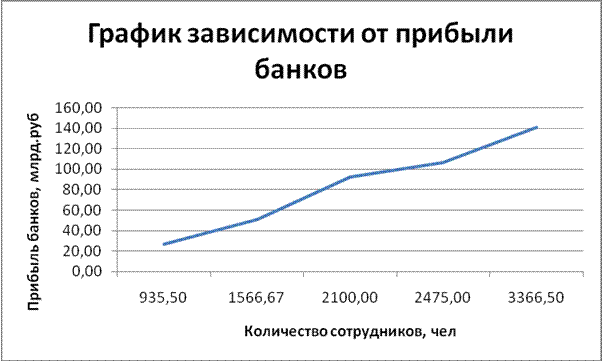
Рисунок №1 – График зависимости прибыли банков от количества сотрудников.

Согласно данным графика видно, что наибольшую прибыль получают банки с наибольшим количеством  сотрудников.

Задача №9  Теплота сгорания нефти равна 45,0 мДж/кг, угля – 26,8 мДж/кг. Сделайте пересчет в условное топливо (29,3 мДж/кг) и рассчитайте цепные и базисные показатели динамики добычи нефти, используя данные таблицы 3.

Таблица 3 - Добыча нефти и угля, млн.т.

Топливо	Объем добычи
	2003 г.	2004 г.	2005 г.
Нефть Уголь	300 250	325 260	350 270

Решение:

1. Переведем значения объемов добычи нефти за 2003, 2004 и 2005 года в условное топливо:

2003 год:  300*45 / 29,3 = 460,8 млн.т.

2004 год: 325*45 / 29,3 = 499,2 млн. т.

2005 год: 350*45 / 29,3 = 537,6 млн. т.

2. Рассчитаем цепные показатели динамики добычи нефти по следующей формуле:

ОПД_ц = Y_i / Y_i-1,                                    (3)

ОПД_05/04 = 537,6 / 499,2 = 1,077*100% = 107,7%

ОПД_04/03 = 499,2 / 460,8 = 1,083*100% = 108,3%

3. Рассчитаем базисные показатели динамики добычи нефти по следующей формуле:

ОПД_б = Y_i / Y₀ ,                                      (4)

ОПД_05/03 = 537,6 / 460,8 = 1,167*100% = 116,7%

ОПД_04/03 = 499,2 / 460,8 = 1,083*100% = 108,3%

Вывод: 1) Добыча нефти в 2004 году по сравнению с 2003 годом возросла на 8,3%. 2) В 2005 году добыча нефти возросла на 7,7% по сравнению с 2004 годом и на 16,7% по сравнению с 2003 годом.

Задача №17   Определить: 1) средние затраты времени на проезд к месту работы у рабочих; 2) среднеквадратическое отклонение и дисперсию; 3) коэффициент вариации.

Таблица 4 - Затраты времени рабочих на проезд к месту работы

Затраты времени, мин	До 30	30-40	40-50	50-60	60-70
Число рабочих	70	80	200	55	15

Решение:

Обозначим: x_i – затраты времени, f_i – число рабочих.

Для определения показателей построим расчётную таблицу 5:

xi	fi	xi	xi f	(xi - i)	(xi - i)2·f
20-30	70	25	1750	- 16,79	19733,287
30-40	80	35	2800	- 6,79	3688,328
40-50	200	45	9000	3,21	2060,82
50-60	55	55	3025	13,21	9597,7255
60-70	15	65	975	23,21	8080,5615
Итого	420	–	17550	–	43160,722

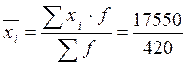 = 41,79 - средние затраты времени на проезд к месту работы у рабочих.

σ² = 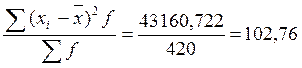 - дисперсия.

=10,14 - среднеквадратическое отклонение.

V = 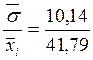· 100% = 24, 26% - коэффициент вариации.

Ответ: средние затраты времени на проезд к месту работы у рабочих 41,79 мин.

Задача №20  В результате выборочного обследования покупателей супермаркета (повторная выборка) получено следующее распределение по размеру  покупок:

Таблица 6 – Исходные данные

Стоимость покупки, р.	До 100	100-200	200-300	300 и более
Число покупателей	37	158	289	143

С вероятностью 0,954 определить:

а) границы среднего размера покупки;

б) границы удельного веса покупок на сумму до 100 р.;

в) число покупателей супермаркета, которых необходимо охватить  в процессе выборочного наблюдения, чтобы с вероятностью 0,997 определить границы среднего размера покупки с предельной ошибкой 15 р.

Решение:

Для определения средней ошибки выборки нам необходимо, прежде всего, рассчитать выборочную среднюю величину и дисперсию изучаемого признака:

Таблица 7 - Расчет среднего размера покупки  и дисперсии

Стоимость покупки, р., х	Число покупателей, f	Середина интервала, х	хf	х2f
До 100	37	50	1850	92500
100-200	158	150	23700	3555000
200-300	289	250	72250	18062500
300 и более	143	350	50050	17517500
Итого	627	-	147 850	39227500

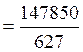_i  = 235, 81;

σ² = 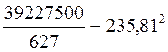 = 6957,44;

σ = = 83,41

Средняя ошибка выборки составит:

μ_х = 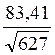 = 3,33 р.

Определим с вероятностью 0,954 (t = 2) предельную ошибку выборки:

 = 2 · 3,33 = 6,66 р.

Установим границы генеральной средней:

235, 81 – 6,66 ≤  ≤ 235, 81 + 6,66

или

229,15 ≤  ≤ 242,47

Таким образом, на основании проведенного выборочного обследования с вероятностью 0,954 можно заключить, что средний размер покупки лежит в пределах от 229,15  до 242,47  рублей.

Для ответа на вопрос, поставленный в пункте «б» данной задачи, по выборочным данным определим долю покупок на сумму до 100 р. и рассчитаем дисперсию доли:

w = = 0,059;

= w(1 – w) = 0,059 *(1-0,059) = 0,0555

Рассчитаем среднюю ошибку выборки:

μ_w = 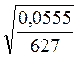 = 0,0094

Предельная ошибка выборки с заданной вероятностью составит:

∆_w = 2 • 0,0094 = 0,0188.

Определим границы генеральной доли:

0,059 – 0,0188 ≤ р ≤ 0,059 + 0,0188

или

0,0402 ≤ р ≤ 0,0778

Следовательно, с вероятностью 0,954 можно утверждать, что доля покупок на сумму до 100 р. находится в пределах от 4,02% до 7,78%.

Для ответа на вопрос, поставленный в пункте «в» данной задачи, будем использовать формулу для расчета объема выборки для определения числа покупателей супермаркета, при повторном отборе:

n_w =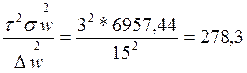

Вывод: Нужно обследовать не менее 278,3 покупателей супермаркета