Методические указания к выполнению расчетно-графического задания по информатике на тему «Системы счисления»

Министерство образования и науки Российской Федерации

Государственное образовательное учреждение

высшего профессионального образования

«Комсомольский-на-Амуре Государственный технический университет»

Методические указания

к выполнению расчетно-графического задания по информатике

на тему «Системы счисления».

Для студентов первого курса ФЭМ

2008 г.

Цель работы: ознакомиться с системами счисления, применяемыми в цифровых системах управления и обработки информации; приобрести навыки перевода чисел из одной системы счисления в другие.

1 СИСТЕМЫ СЧИСЛЕНИЯ

1.1 Позиционные и непозиционные системы счисления

Под системой счисления вообще понимается способ представления любого числа посредством некоторого алфавита символов, называемых в данном случае цифрами.

Существует два типа систем счисления: позиционные и непозиционные. Примером непозиционной системы счисления является римская система записи и представления чисел. Она является непозиционной, потому что каждая цифра всегда имеет одно и то же значение, независимо от места в записи числа. Так, Х в этой системе всегда будет означать десяток, не смотря на место, где стоит этот символ в числе.

Позиционной системой счисления является так называемая арабская система записи чисел. Одна и та же цифра из десяти (0,1,2,3,4,5,6,7,8,9) будет иметь различное значение в зависимости от места, на котором она находится в числе. В числе 123 единица означает количество сотен, двойка - количество десятков, тройка – количество единиц.

Количество цифр, используемое для записи чисел позиционной системы счисления, называется основанием. В рассмотренной выше системе основанием является число десять: это цифры от 0 до 9. Если основание системы счисления обозначить S, то в общем случае любое число в любой позиционной системе счисления можно представить в виде полинома от соответствующего основания:

В качестве коэффициентов а_i могут стоять любые из S цифр, используемых в данной системе.

В простой записи чисел позиционных систем любое число записывают в форме  Запятая в такой форме отделяет целую часть от дробной. Дробной частью числа являются слагаемые полинома, имеющие степень основания меньше нуля.

1.2 Двоичная система счисления

В этой системе используется только две («двоичные») цифры: 0 и 1. Именно такое представление чисел в виде электрических сигналов наиболее оптимально для цифровых вычислительных устройств. В первую очередь это связано с высокой помехоустойчивостью таких электрических сигналов. Во-вторых, реализация цифровых вычислителей гораздо проще, чем аналоговых, что во многом определяется первым замечанием.

В двоичной системе счисления любое число может быть представлено последовательностью двоичных цифр:

, где  β_i - либо 0, либо 1.

Эта запись соответствует сумме степеней числа 2, взятых с указанными в ней коэффициентами:

Например, число (101101,101)₂ представляется суммой:

(101101,101)₂ = 1∙2⁵+0∙2⁴+1∙2³+1∙2²+0∙2¹+1∙2⁰+1∙2^-1+0∙2^-2+1∙2^-3

Таким образом можно вычислить соответствующее значение его в десятичной системе счисления:

32+8+4+1+0,5+0,125=(45,625)₁₀.

1.3 Восьмеричная система счисления

В восьмеричной системе счисления употребляется восемь цифр: 0, 1, 2, 3, 4, 5, 6, 7. Любое число в восьмеричной системе счисления представляется последовательностью цифр:

, где  - цифры от 0 до 7.

1.4 Шестнадцатеричная  система счисления

В шестнадцатеричной системе счисления для изображения чисел употребляется 16 цифр: от 0 до 15. Для обозначения двузначных чисел в данной системе счисления используют латинские буквы от A до F. Таким образом, алфавит системы счисления состоит из следующих цифр:

0 1 2 3 4 5 6 7 8 9 A B C D E F

1.5 Взаимное соответствие чисел в системах счисления

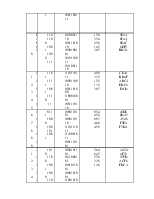
Шестнадцатеричная и восьмеричная системы счисления применяются для упрощенной записи чисел двоичной системы (например, для анализа содержимого ячеек памяти ЭВМ при отладке программы). Между числами этих систем счисления существует простое соответствие, которое объясняется тем, что системы счисления имеют основания, кратные 2: 8=2³, 16=2⁴. В таблице 1 показаны эти соответствия.

Таблица 1.