






ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ РФ
НОВОСИБИРСКИЙ ТЕХНОЛОГИЧЕСКИЙ ИНСТИТУТ
МОСКОВСКОГО ГОСУДАРСТВЕННОГО УНИВЕРСИТЕТА
ДИЗАЙНА И ТЕХНОЛОГИИ
(филиал)
к выполнению расчетно-графической работы по
«Теоретической механике»
для студентов дневной и заочной форм обучения специальность: 170700 – "Машины и аппараты текстильной и легкой промышленности"
УДК: : 531.8
д.т.н., проф. Красюк А.М.
Рецензент:
к.т.н., доцент Ермолаев В.Ф.
Зав.кафедрой Механики к.т.н., доцент Ермолаев В.Ф.
Аналитическое исследование кинематики плоских механизмов. Методические указания к выполнению расчетно-графической работы по «Теоретической механике» - Новосибирск, НТИ МГУДТ (филиал), 2008.
ВВЕДЕНИЕ
Целью выполняемой работы является развитие навыков аналитического исследования кинематики плоских механизмов при помощи ЭВМ.
Студенту предлагается вариант задачи, состоящего из кинематической схемы и таблицы параметров. Варианты заданий берутся из книги Яблонский А.А. и др. Сборник заданий для курсовых работ по теоретической механике: Учеб. пособие для техн вузов/ А.А. Яблонский, С.С. Норейко, С.А. Вольфсон и др.; Под ред.. А.А.Яблонского.- 4-е изд., перераб и доп.. - М.: Высш. шк., 1985. – 367 с., и последующие издания. Для механизма необходимо составить систему линейных алгебраических уравнений и решить ее на ЭВМ. Результат работы оформить и сдать преподавателю для зачета.
Расчетно-графическая работа предполагает выполнение трех этапов: подготовительного, этапа решения задачи на ЭВМ и оформления отчета.
Известно, что скорость
любой точки В плоской фигуры геометрически складывается из скорости
какой-нибудь другой точки А, принятой за полюс, и скорости, которую
точка В получает при вращении фигуры вокруг этого полюса, т.п. ![]() или
или ![]() .
.
Уравнения скоростей точек механизма получаются последовательным от звена к звену, применением этой формулы. Рассмотрим пример. Пусть для механизма, представленного на рисунке 1 требуется определить скорость ползуна D в любой момент времени.
![]() ;
;
![]()
![]() ;
;
![]()
![]() :
:
![]()
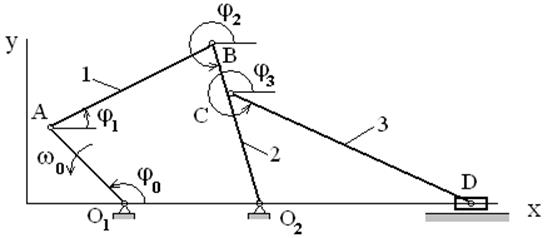 |
Для начала вычертим этот
механизм в масштабе (удобнее выполнять на миллиметровой бумаге , т.к. для
решения потребуется транспортиром определить начальные углы ![]() .
.
Обозначим звенья цифрами, что несколько упростит запись уравнений. Пусть ведущее звено ОА будет нулевым, звено АВ - №1, О2В - №2, СД - №3, Д - №4.
Скорость точки А
легко определить как ![]() .
.
Для определения скоростей других точек сначала запишем уравнения внешних связей, накладываемых на механизм
![]() .
(1)
.
(1)
Теперь составим уравнения для всех точек
![]() ;
;
![]() ;
(2)
;
(2)
![]() ;
;
![]() .
.
Но эти уравнения векторные. И для того, чтобы ими можно было воспользоваться, сделаем их скалярными, спроецировав на координатные оси Х и У.
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
(3)
;
(3)
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
Теперь запишем систему уравнений (1) с учетом полученных выражений (3).
Замечание: систему уравнений следует записать в виде:
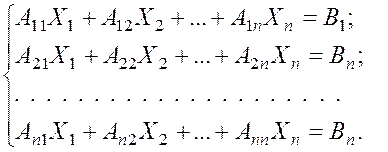
Получим:
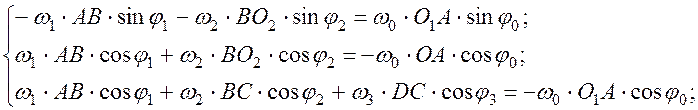 (4)
(4)
где ![]()
![]() .
.
![]() ;
;
![]() ;
; ![]() ;
; ![]() ;
;
![]() ;
;
![]() ;
; ![]() ;
; ![]() ;
;
![]() ;
;
![]() ;
; ![]() ;
; ![]() .
.
В дальнейшем нам
потребуются значения углов ![]() в начальный момент
времени. Определим их либо аналитически, либо графические (транспортиром). На
этом подготовительный этап заканчивается.
в начальный момент
времени. Определим их либо аналитически, либо графические (транспортиром). На
этом подготовительный этап заканчивается.
Система линейных алгебраических уравнений (4) может быть решена различными способами. Наиболее подходящим является метод Гаусса с выбором главного элемента. Это обусловлено тем, что он наиболее устойчив при решении разряженных матриц. Для повышения устойчивости решения следует к значениям углов кратным 90О прибавить незначительную погрешность. Например, вместо угла 270О следует записать 270,5О, такие изменения практически не повлияют на результат, но существенно повысят устойчивость решения.
Решение системы уравнений
(4) даст значения угловых скоростей звеньев только для начального положения
механизма. Примем допущение, что в течение малого промежутка времени Dt угловые скорости не изменяются.
Тогда за этот промежуток времени звенья механизма повернуться на угол ![]() , где i - номер звена, а новые значения углов будут иметь
значения
, где i - номер звена, а новые значения углов будут иметь
значения ![]() . После этого вновь пересчитываются коэффициенты
матрицы находятся значения угловых скоростей звеньев для нового положения
механизма. Расчет ведется до тех пор, пока ведущее звено не сделает полный
оборот. Величину Dt
следует выбирать не более, чем 1/20 времени полного оборота ведущего звена.
. После этого вновь пересчитываются коэффициенты
матрицы находятся значения угловых скоростей звеньев для нового положения
механизма. Расчет ведется до тех пор, пока ведущее звено не сделает полный
оборот. Величину Dt
следует выбирать не более, чем 1/20 времени полного оборота ведущего звена.
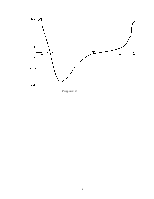
По результатам расчета строится график зависимости угловой скорости звена или линейной скорости точки от угла поворота ведущего звена (см. рисунок 2). Номер звена или точка задается преподавателем индивидуально каждому студенту.
Для проверки правильности численного решения необходимо построить план скоростей механизма для его начального положения. Ошибка между численным и графическим решением не должна превышать 5%.
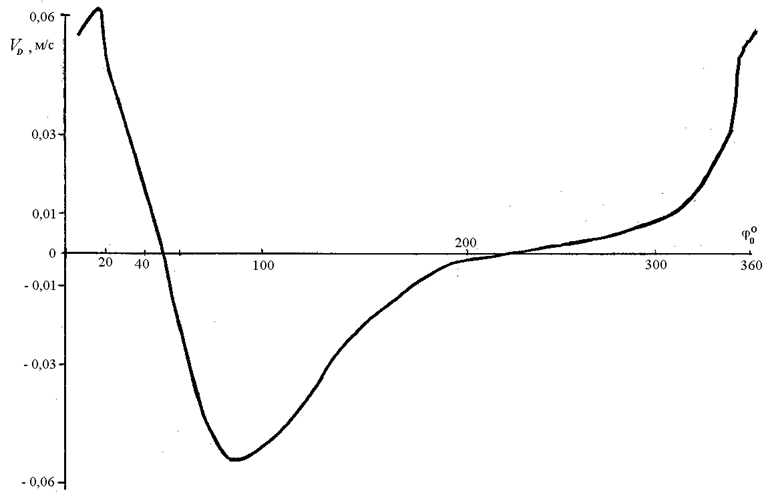 Рисунок 2
Рисунок 2
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.