Дифференциальное уравнение движения груза, входящего в состав механической системы с блоком

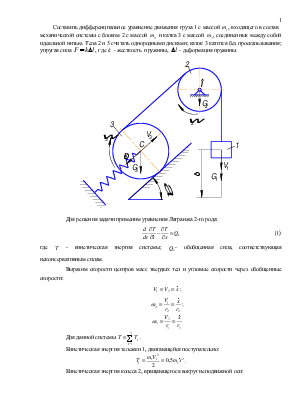
Составить дифференциальное уравнение движения груза 1 с массой , входящего в состав механической системы с блоком 2 с массой  и катка 3 с массой , соединенных между собой идеальной нитью. Тела 2 и 3 считать однородными дисками; каток 3 катится без проскальзывания;   упругая сила , где  - жесткость  пружины,  - деформация пружины.

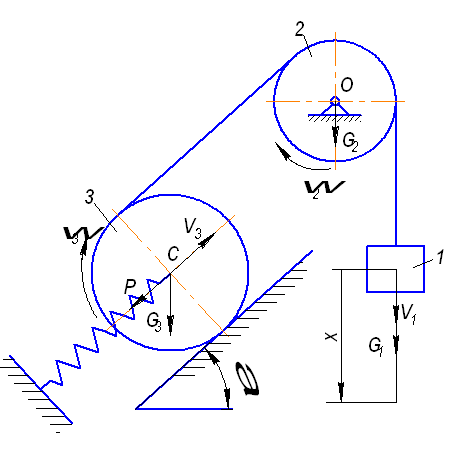
Для решения задачи применим уравнения Лагранжа 2-го рода:

где  - кинетическая энергия системы; - обобщенная сила, соответствующая неконсервативным силам.

Выразим скорости центров масс твердых тел и угловые скорости через обобщенные скорости:

;

;

Для данной системы .

Кинетическая энергия тележки 1, двигающейся поступательно:

.

Кинетическая энергия колеса 2, вращающегося вокруг неподвижной оси:

,

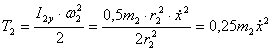где  - момент инерции тела 2.

Кинетическая энергия колеса 3, совершающего плоское движение:

,

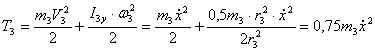где  - момент инерции тела 3.

Тогда