Расчет плоской рамы методом сил (внешние нагрузки: Р = 10 кН, q = 32 кН/м, длины стержней - 2,5 м)

Расчет плоской рамы методом сил

Исходные данные: расчетная схема рамы приведена на рисунке 1. Внешние нагрузки: Р = 10 кН,  q = 32 кН/м; длины стержней  l = 2,5 м, угол α = 22⁰; жесткость EJ = 10⁷ Н ∙ м².

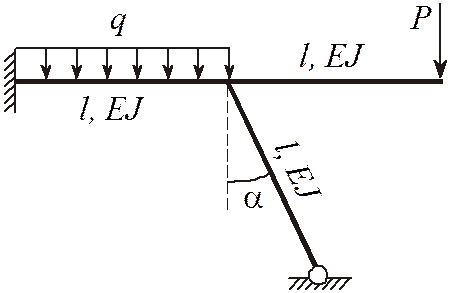
Рисунок 1

1.Вычисление степени статической неопределимости.Схема опирания плоской рамы изображена на рисунке2. Степень ее статической неопределимости вычислим по формуле:

s = 3К – Ш = 3 ∙ 1 – 1 = 2.

Здесь К – число замкнутых контуров, Ш – количество простых шарниров. Так как s = 2, то система два раза статически неопределима.

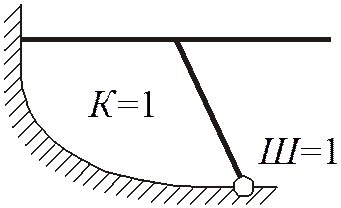
Рисунок 2

2.Выбор основной системы.

Основная система (о.с.) метода сил – это статически определимая система, полученная из заданной путем отбрасывания лишних связей.

Для того, чтобы основная и заданная системы были эквивалентными, к основной системе, кроме внешней нагрузки, прикладывают дополнительные усилия, представляющие собой реакции отброшенных связей.

Приведем три варианта основной системы (рисунок 3, а, б, в). Поясним каждый из них. В I-м случае отбрасываем шарнирно-неподвижную опору. Получаем ломаный брус, заделанный левым концом, к которому дополнительно  приложены  две  неизвестные  сосредоточенные  силы X₁, X₂. Во II-м случае жесткую заделку заменяем стержнем. При этом к системе прикладываем неизвестные силу X₁ и момент X₂. Вариант III получаем, заменяя заделку шарнирно-неподвижной опорой и вводя простой шарнир в верхнее сечение наклонного элемента рамы. В качестве неизвестных прикладываем сосредоточенный момент X₁, а также два равных и противоположно направленных момента X₂. (Усилие X₂ имеет смысл внутреннего изгибающего момента, т. е. при составлении уравнений равновесия всей системы его суммарный момент будет равен нулю).

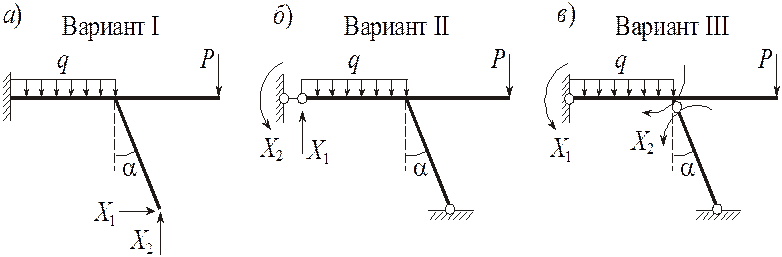
Рисунок 3

Для расчета выбираем третий вариант о.с., так как эпюры изгибающих моментов для него получатся наиболее простыми. Следовательно, при их перемножении количество подсчетов будет наименьшим.

Проводим кинематический анализ принятой основной системы. Число степеней свободы определяем по формуле Чебышева:

W = 3Д – 2Ш – С_оп,

где Д – количество дисков, Ш – количество шарниров, С_оп – число опорных стержней. Для рассматриваемой рамы, представленной в виде дисков D₁ и D₂  (рисунок 4),  Д = 2, Ш = 1, С_оп = 4,  следовательно, W = 3 ∙ 2 – 2 ∙ 1 – 4 = 0. То есть, система статически определима.

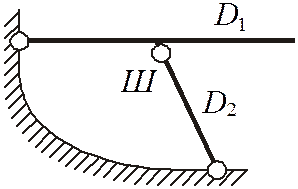
Рисунок 4

Анализируем геометрическую структуру конструкции. Она представляет собой диск D₁, присоединенный к земле с помощью шарнира и стержня (диска D₂), причем ось стержня не проходит через шарнир. Значит, выбранная основная система метода сил геометрически неизменяема.

3.Составление системы канонических уравнений.

Рама два раза статически неопределима, следовательно, канонические уравнения представляют собой систему двух линейных уравнений с двумя неизвестными:

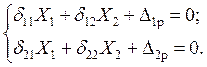                                         (1)

Здесь  X₁, X₂ – неизвестные усилия;  δ₁₁, δ₂₂ – главные единичные перемещения; δ₁₂, δ₂₁ – побочные единичные перемещения, в соответствии с теоремой Максвелла δ₁₂ = δ₂₁;   Δ_1p, Δ_2p – грузовые перемещения по направлениям усилий X₁, X₂ от внешней нагрузки.

Для определения перемещений δ₁₁, δ₁₂, δ₂₁, δ₂₂, Δ_1p, Δ_2p по формуле Мора необходимо построить единичные и грузовую эпюры изгибающих моментов.

4.Построение единичных и грузовой эпюр изгибающих моментов

Построение единичной эпюры .

Эпюру  строим в основной системе от воздействия единичного усилия .  В опорных шарнирах  А и В    возникают  четыре  составляющие  опорных реакций Z_A, Y_A, Z_B, Y_B  (рисунок 5, а).Нет необходимости вычислять их все. Определим только те, которые нужны для расчета ординат эпюры .Мысленно проведем горизонтальное сечение по шарниру С и составим уравнение равновесия верхней части:,  ,

отсюда  .В каждой из характерных точек 1, …, 6  вычислим значение ординат эпюры  (k – номер точки).   При  этом  подсчитаем   только  абсолютные значения моментов и укажем, какие волокна они растягивают. (растянуты левые волокна); ;. По полученным ординатам строим эпюру  (рисунок 5, б). Следует заметить, что эпюра безразмерная, так как она построена от воздействия единичного изгибающего момента .

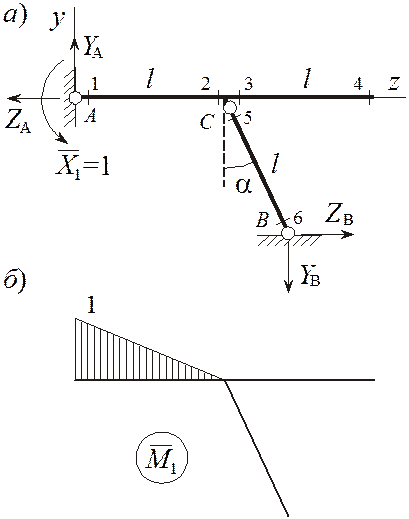
Рисунок 5

Построение единичной эпюры .Эпюру  строим аналогично эпюре , только от воздействия единичного усилия  (рисунок 6,а). Определим необходимые составляющие опорных реакций.Мысленно разрежем раму горизонтальным сечением по шарниру С и рассмотрим равновесие нижней части. В ней будет действовать один из моментов  (нижний). Составим уравнение статики ,  , отсюда  .В каждой из точек 1, …, 6 вычислим значение изгибающего момента  (k – номер точки). ;  (растянуты правые волокна); . Для определения момента  проведем сечение в 5-й точке и рассмотрим равновесие нижней части. Получим:  (растянуты верхние волокна).По вычисленным ординатам строим эпюру  (рисунок 6,б). Она также безразмерная.

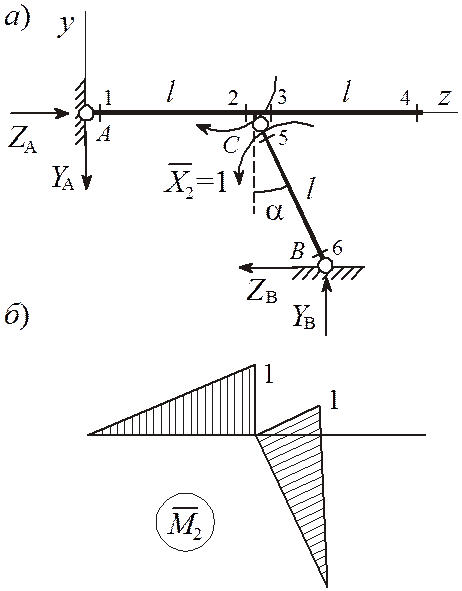
Рисунок 6

Построение грузовой эпюры М_р.

Эпюру М_р строим в основной системе от внешней нагрузки. Покажем в опорных шарнирах  А и В составляющие опорных реакций: Z_A, Y_A, Z_B, Y_B  (рисунок 7, а). Для расчета ординат эпюры М_р достаточно определить только Y_В.

Мысленно проведем горизонтальное сечение по шарниру С и составим уравнение равновесия верхней части:,  ,

отсюда   кН.

В  каждой  из  характерных  точек 1, …, 6  вычислим значение изгибающего момента М_р^(k) (k – номер точки).М_р⁽¹⁾ = М_р⁽⁴⁾ = М_р⁽⁶⁾ = 0;

М_р⁽²⁾ = -Y_Вl + ql²/2 = – 30 ∙ 2,5 + 32 ∙ 2,5²/2 =25 кН ∙ м (растянуты верхние волокна);

М_р⁽³⁾ = Рl = 10 ∙ 2,5 = 25 кН ∙ м (растянуты верхние волокна);

М_р⁽⁵⁾ ==.

Откладываем полученные ординаты на эпюре М_р (рисунок 7, б). В пределах участка 1–2 эпюра ограничена параболой, направленной выпуклостью вниз. Максимум не определяем, так как он не понадобится в дальнейших расчетах. На участках 3–4 и 5–6 эпюра прямолинейна.

Дополнительно вычислим значение момента М_р⁽⁷⁾ в точке 7 (посередине участка 1–2),  так как  оно  понадобится  при перемножении эпюр.

М_р⁽⁷⁾ = Y_Вl/2 – q(l/2)²/2 = 30 ∙ 2,5/2 – 32 ∙ (2,5/2)²/2 = 12,5 кН ∙ м

(растянуты нижние волокна).

Рисунок 7

5.Вычисление единичных и грузовых перемещений.

Для определения перемещений, являющихся коэффициентами канонических уравнений, используем формулу Мора. При этом влиянием продольных и поперечных сил пренебрегаем и считаем, что перемещения обусловлены только действием изгибающих моментов. Используем следующие формулы:

, , ,

, .

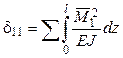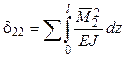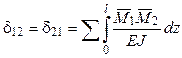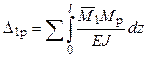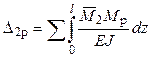Так как все три стержня рамы прямолинейны и их жесткость постоянна, перемещения вычислим способом перемножения эпюр Верещагина.

Чтобы определить единичное перемещение δ₁₁, необходимо эпюру