








Усилия в стержнях ригеля определяем от постоянной и снеговой нагрузок, а также от опорных моментов, возникающих в раме в результате жёсткого соединения ригеля с колоннами.
Усилия в ригеле определяем графическим способом по диаграмме Максвелла – Кремона.
Усилия в любом стержне фермы от опорных моментов вычисляются по формуле:
![]()
а в нижнем поясе с учётом нормальной силы по формуле:
![]()
Где
Расчётные усилия определяем в табличной форме.
![]() кН,
кН,
![]() кН.
кН.
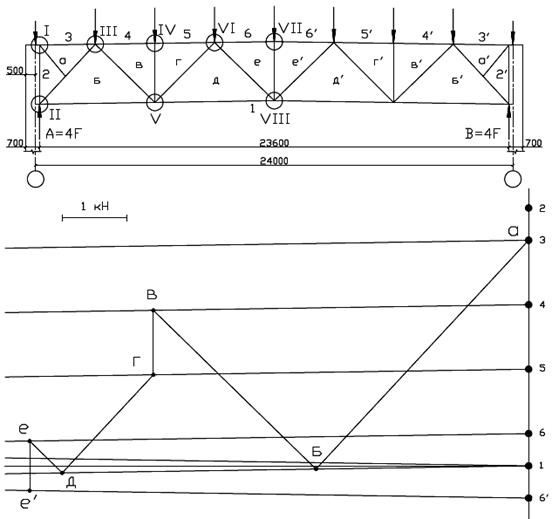
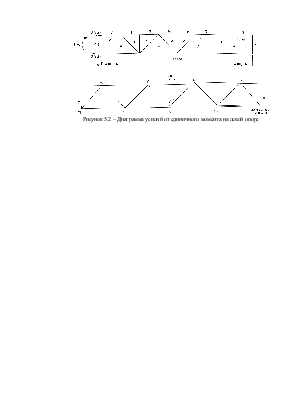
Рисунок 5.1 – Диаграмма усилий от вертикальной нагрузки
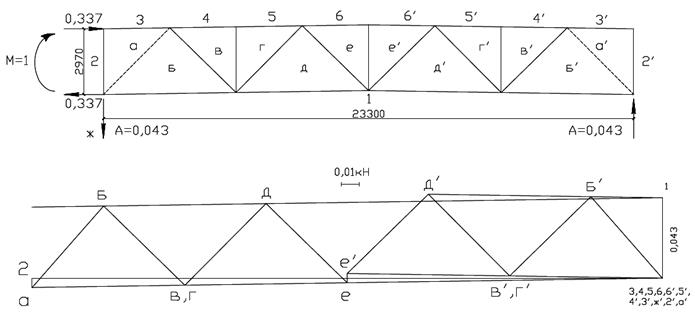
Рисунок 5.2 – Диаграмма усилий от единичного момента на левой опоре
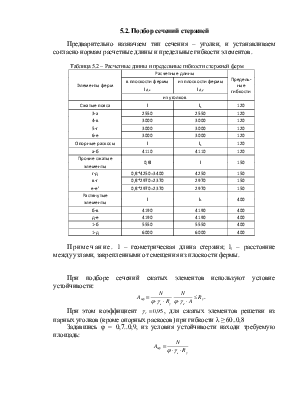
Предварительно назначаем тип сечения – уголки, и устанавливаем согласно нормам расчетные длины и предельные гибкости элементов.
Таблица 5.2 – Расчетные длины и предельные гибкости стержней ферм
|
Элементы ферм |
Расчетные длины |
Предель-ные гибкости |
|
|
в плоскости фермы |
из плоскости фермы |
||
|
lef,x |
lef,y |
||
|
из уголков |
|||
|
Сжатые пояса |
l |
l1 |
120 |
|
3-а |
2550 |
2550 |
120 |
|
4-в |
3000 |
3000 |
120 |
|
5-г |
3000 |
3000 |
120 |
|
6-е |
3000 |
3000 |
120 |
|
Опорные раскосы |
l |
l1 |
120 |
|
а-б |
4110 |
4110 |
120 |
|
Прочие сжатые |
0,8l |
l |
150 |
|
элементы |
|||
|
г-д |
0,8*4250=3400 |
4250 |
150 |
|
в-г |
0,8*2970=2370 |
2970 |
150 |
|
е-е' |
0,8*2970=2370 |
2970 |
150 |
|
Растянутые |
l |
l1 |
400 |
|
элементы |
|||
|
б-в |
4190 |
4190 |
400 |
|
д-е |
4190 |
4190 |
400 |
|
1-б |
5550 |
5550 |
400 |
|
1-д |
6000 |
6000 |
400 |
Примечание. l – геометрическая длина стержня; l1 – расстояние между узлами, закрепленными от смещения из плоскости фермы.
При подборе сечений сжатых элементов используют условие устойчивости:
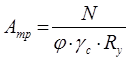
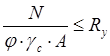 .
.
При этом коэффициент ![]() , для
сжатых элементов решетки из парных уголков (кроме опорных раскосов) при
гибкости λ ≥ 60..0,8
, для
сжатых элементов решетки из парных уголков (кроме опорных раскосов) при
гибкости λ ≥ 60..0,8
Задавшись φ = 0,7..0,9, из условия устойчивости находи требуемую площадь:
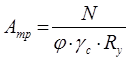
По сортаменту подбирают подходящий профиль и вычисляем гибкости в двух плоскостях
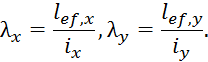
По большей гибкости находим φ, проверяем устойчивость и при необходимости корректируем сечение, добиваясь более полного использования материала.
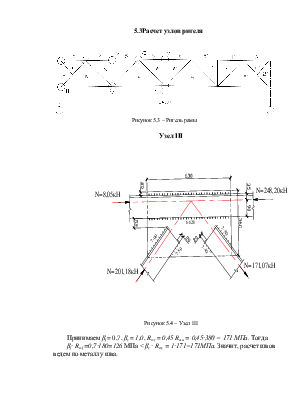
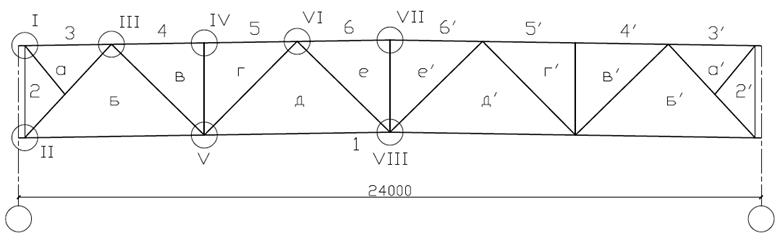 Рисунок 5.3 – Ригель рамы
Рисунок 5.3 – Ригель рамы
Узел III
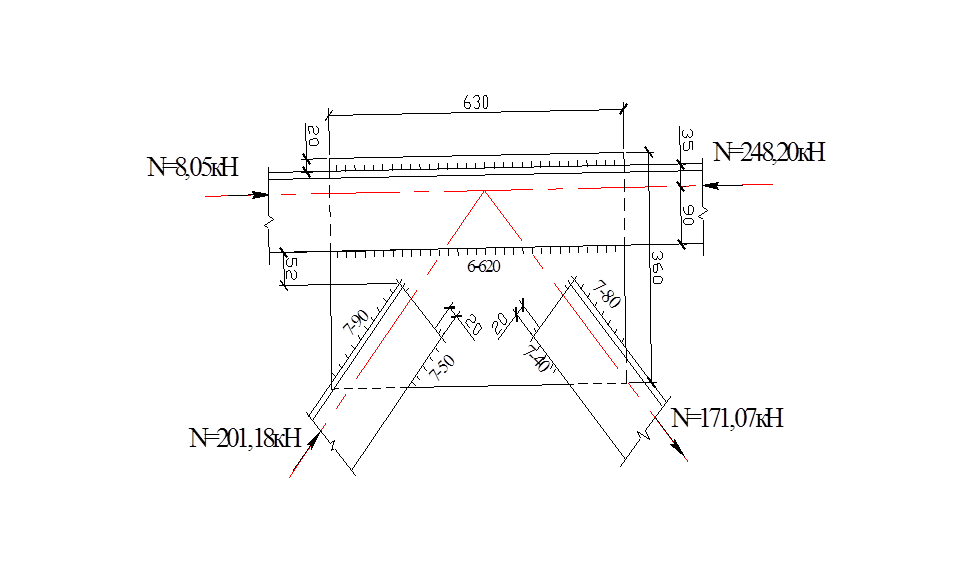
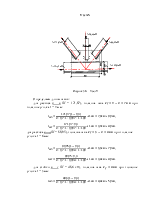
Рисунок 5.4 – Узел III
Принимаем βf = 0,7, βz = 1,0, Rwz = 0,45 Run = 0,45∙380 = 171 МПа. Тогда
βf∙ Rwf =0,7∙180=126 МПа < βz ∙ Rwz = 1∙171=171МПа. Значит, расчет швов ведем по металлу шва.
Длины швов по обушку и перу будут определены из условий:
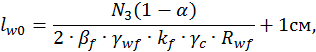
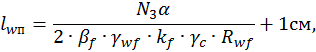
где α – отношения, изменяемое для уголков в пределах 0,25…0,32, принято α = 0,3;
Определяем длины швов:
Для раскоса а – б(N = 201,18), толщина
шва ![]() при толщине уголка t
= 9 мм:
при толщине уголка t
= 9 мм:
![]()
![]()
для раскоса б – в(N = 171,07):
![]()
![]()
Фасонку к поясным уголкам прикрепляют четырьмя швами,
толщину которых рассчитывают на узловую силу от постоянной и снеговой нагрузок
(![]() ) и
сдвигающее усилие (
) и
сдвигающее усилие (![]() ) по
формуле:
) по
формуле:
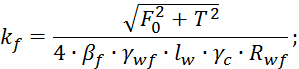
где
![]()
![]()
Тогда катет шва
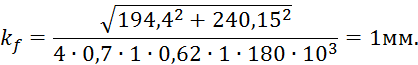
Принимаем ![]()
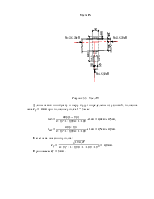
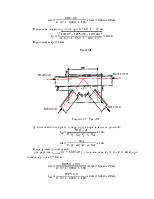
Узел IV
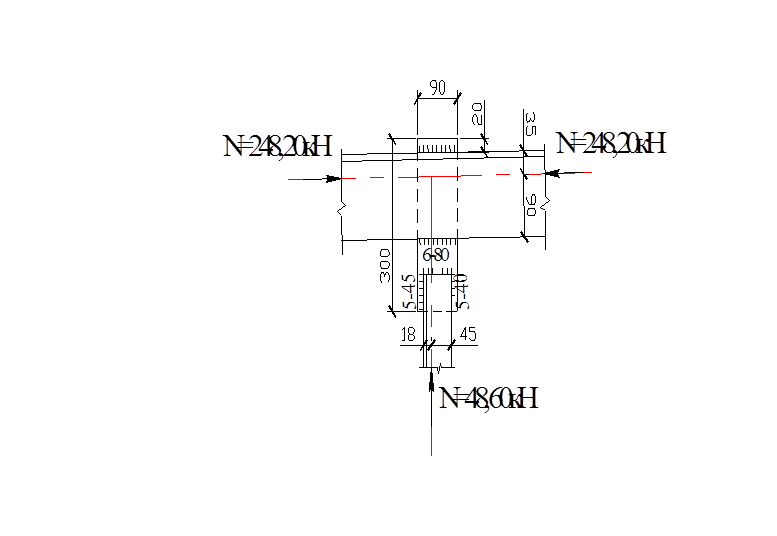
Рисунок 5.5 – Узел IV
Длины швов по обушку и перу будут определены из условий,
толщина шва ![]() при толщине уголка t
= 5 мм:
при толщине уголка t
= 5 мм:
![]()
![]()
Катет шва поясного уголка:
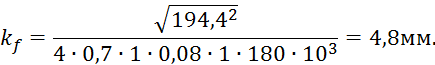
Принимаем ![]()
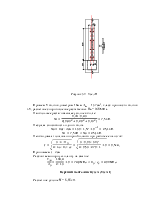
Узел V
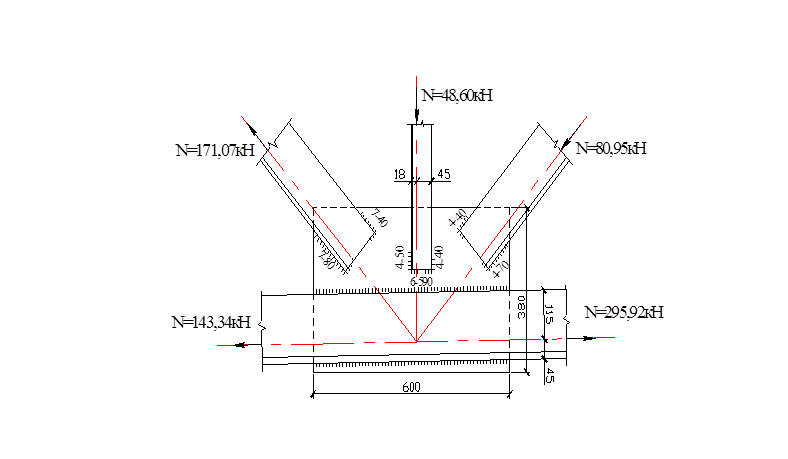
Рисунок 5.6 – Узел V
Определяем длины швов:
для раскоса б – в (N = 171,07), толщина
шва ![]() при толщине уголка t
= 9 мм:
при толщине уголка t
= 9 мм:
![]()
![]()
для раскоса г
– д (N
= 80,95), толщина шва ![]() при толщине уголка t = 6 мм:
при толщине уголка t = 6 мм:
![]()
![]()
для стойки в – г (N = 48,6 кН), толщина
шва ![]() при толщине уголка t
= 5 мм:
при толщине уголка t
= 5 мм:
![]()
![]()
Катет шва поясного уголка при lw = 60 −1 = 59 см:
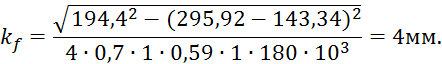
Принимаем ![]()
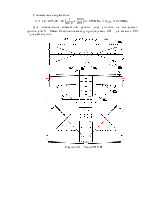
Узел VI
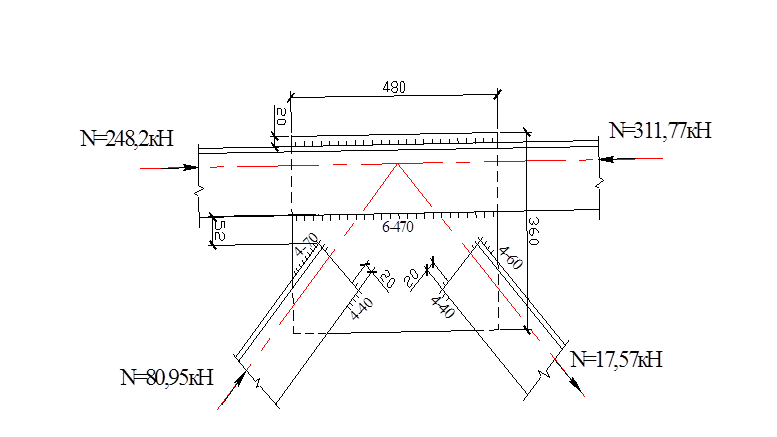
Рисунок 5.7 – Узел VI
Длины швов по обушку и перу будут определены из условий:
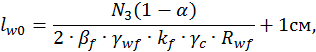
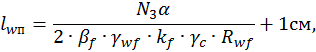
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.