




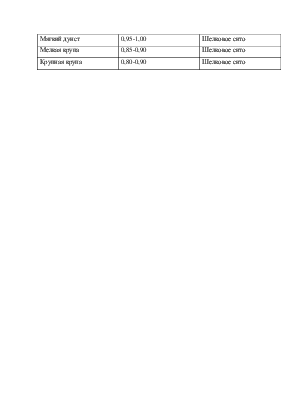



Послойное движение сыпучего материала.
При достаточной площади горизонтальной опорной поверхности, совершающей круговые поступательные колебания, сыпучий материал располагается на ней в виде сыпучего тела, толщину которого будем считать одинаковой над всеми точками поверхности, так же как гранулометрический состав и свойства частиц. Частицы, расположенные в верхнем слое сыпучего тела,
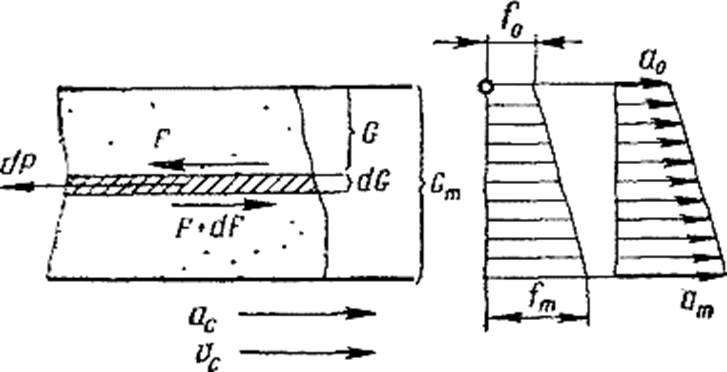
Рис 20 Схема послойного движения сыпучего тела при прямолинейном ускоренном движении. отличаются большей подвижностью сравнительно с частицами внутри сыпучего тела и особенно с частицами нижнего слоя. Это объясняется увеличением числа связей частиц по мере удаления их от свободной поверхности, и при теоретическом рассмотрении может быть учтено увеличением коэффициентов трения нижележащих слоев.
Полагая толщину сыпучего тела намного меньшей горизонтальных размеров опорной поверхности, рассмотрим его как совокупность бесконечно большого числа слоев — пластин, равных по весу dG (отнесенному к единице опорной площади). При этом примем коэффициент сопротивления сдвигу слоев (коэффициент трения) непрерывной возрастающей функцией веса вышележащей части сыпучего тела.
На рисунке 20 показана схема послойного движения сыпучего тела при прямолинейном равноускоренном движении опорной поверхности; с наибольшими скоростью и ускорением движется нижний слой, с наименьшими - верхний.
Рассмотрим условия динамического
равновесия элементарного слоя внутри сыпучего тела, скорость которого больше,
чем вышележащего, но меньше, чем нижележащего. Поэтому сила трения F со стороны вышележащего слоя
препятствует движению, а сила трения F+dF со стороны нижележащего слоя
способствует движению. Разность этих сил уравновешена силой инерции ![]() , где а — ускорение рассматриваемого слоя.
, где а — ускорение рассматриваемого слоя.
Имеем dP = dF или ![]() dG = dF,
откуда
dG = dF,
откуда
![]() (131)
(131)
Так как F=fG, где f— коэффициент сопротивления сдвигу в данном слое, a G — вес вышележащей части сыпучего тела, то
![]() (132)
(132)
Поскольку f — возрастающая функция G, то приведенный коэффициент
сопротивления сдвигу слоев f![]() >f и
тоже возрастает, но более прогрессивно по мере приближения слоя к опорной поверхности.
Для зерна и продуктов его переработки зависимость f(G) близка к
линейной и аппроксимируется уравнением
>f и
тоже возрастает, но более прогрессивно по мере приближения слоя к опорной поверхности.
Для зерна и продуктов его переработки зависимость f(G) близка к
линейной и аппроксимируется уравнением
f=f![]() +cG. (133) .
+cG. (133) .
Введем обозначения
![]() j=
j=![]() и
и ![]() , где G и
, где G и ![]() — давления соответственно вышележащей части и всего
сыпучего тела;
— давления соответственно вышележащей части и всего
сыпучего тела;
![]() и
и ![]() — коэффициенты сопротивления сдвигу
соответственно верхнего и нижнего слоев.
— коэффициенты сопротивления сдвигу
соответственно верхнего и нижнего слоев.
Тогда зависимости (131) и (132) принимают вид
![]() (134)
(134)
и
![]() (135)
(135)
Так как на нижний элементарный слой при предельном установившемся движении системы действуют в горизонтальной плоскости постоянные силы трения, то при круговых колебаниях опорной поверхности их равнодействующую можно рассматривать как центростремительную силу. Тогда все элементарные слои, как бесконечно тонкие пластины, совершают круговое поступательное движение, характеризуемое радиусами r, вокруг неподвижных точек.
Разрыхление и процесс самосортирования в сыпучем теле, состоящем из частиц одинаковой плотности, но различных размеров, зависит от интенсивности послойного движения, которую определяют как относительную скорость двух смежных слоев, деленную на вес элементарного слоя dG,
![]() . (151)
. (151)
Если радиусы траекторий смежных
слоев в абсолютном движении r и r+dr (см.рис.21 и22,б), то радиус их траектории в относительном
движении составляет ![]() .Поэтому
.Поэтому
![]() и
и ![]() .
(152)
.
(152)
Продифференцируем выражение (141)
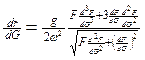 . (153)
. (153)
Выражая sin![]() через cos
через cos![]() , получим из (144)
, получим из (144)
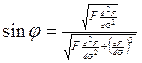 . (154)
. (154)
Тогда уравнение (152) принимает вид
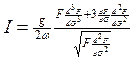 . (155)
. (155)
Так как сила трения F и ее производные при ![]() не зависит от кинематических параметров,
то интенсивность послойного движения обратно пропорциональная
не зависит от кинематических параметров,
то интенсивность послойного движения обратно пропорциональная ![]() , а следовательно, при
, а следовательно, при ![]() пропорциональна
пропорциональна ![]() .
Затем можно выводы.
.
Затем можно выводы.
1. Послойное движение сыпучего тела при достаточной площади опорной горизонтальной поверхности возможно лишь при условии, что коэффициент сопротивления сдвигу вышележащих слоев.
2.
При постепенном
увеличении ускорения опорной поверхности относительное движение слоев сыпучего
тела начинается сверху при первом критическом ускорении ![]() и постепенно распространяется вниз; при
втором критическом ускорении
и постепенно распространяется вниз; при
втором критическом ускорении ![]() начинается относительное
движение нижнего слоя по опорной поверхности. В области ускорений
начинается относительное
движение нижнего слоя по опорной поверхности. В области ускорений ![]() послойное движение происходит лишь в части
сыпучего тела.
послойное движение происходит лишь в части
сыпучего тела.
3.
Интенсивность
послойного движения при ![]() обратно пропорциональна
угловой скорости
обратно пропорциональна
угловой скорости ![]() и в среднем для всего сыпучего
тела имеет максимум при
и в среднем для всего сыпучего
тела имеет максимум при ![]() .
.
4.
Скорость частиц
нижнего слоя относительно опорной поверхности при неизменном ускорении ![]() пропорциональна радиусу R колебаний опорной поверхности.
пропорциональна радиусу R колебаний опорной поверхности.
Полученные формулы, характеризующие
послойное движение в сыпучем теле, справедливы при указанных выше условиях для
любой зависимости ![]() , если она монотонно возрастает.
В частности, если
, если она монотонно возрастает.
В частности, если ![]() -линейная функция, как это имеет
место приближенно для зерна и продуктов его переработки в известных пределах
толщины сыпучего тела, то параметры его послойного движения можно выразить через
показатели механических свойств
-линейная функция, как это имеет
место приближенно для зерна и продуктов его переработки в известных пределах
толщины сыпучего тела, то параметры его послойного движения можно выразить через
показатели механических свойств ![]() и
и ![]() и переменную
и переменную ![]() ,
,
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.