Элементы общей алгебры. Алгебра логики. Понятия алгебры логики

Элементы общей алгебры. Алгебра логики

Всюду определённая (тотальная) функция      называется n-арной операцией на М.

Если операция бинарная , то будем писать .  - знак операции.

Примеры операций:

1.   на R.

2.   на Z.

3.   на R.

Свойства бинарных операций:

1.  Ассоциативность  для    ;

2.  Коммутативность  для      

3.  Дистрибутивность слева

4.  Дистрибутивность справа

5.  Поглощение

6.  Идемпотентность

Примеры:

1.  Ассоциативные операции: сложение и умножение чисел, пересечение и объединение множеств, композиция отношений. Не ассоциативные – возведение в степень чисел, вычитание множеств.

2.  Коммутативные – сложение и умножение чисел, объединение и пересечение множеств. Не коммутативные – умножение матриц, композиция отношений.

3.  Дистрибутивные – умножение относительно сложения чисел, возведение в степень. Дистрибутивно справа  относительно умножения, но не дистрибутивно слева .

4.  Пересечение поглощает объединение, объединение поглощает пересечение. Сложение и умножение не поглощают друг друга.

5.  Идемпотентные операции – НОД чисел, объединение и пересечение множеств. Не идемпотентные – сложение и умножение чисел.

Множество М вместе с набором операций на нём  называется алгебраической структурой или алгеброй. Множество М – носитель, множество операцийS - сигнатура. Обозначается .

Пример:   - алгебра натуральных чисел.

Гомоморфизмом из А в В называется такая , что для     ,              где  и   -  две алгебры одного типа.

Условие гомоморфизма можно переписать так  или изобразить на диаграмме.

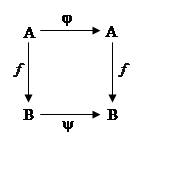
Если на этой диаграмме выбрать некоторый элемент  и двигаться двумя различными путями, то получиться один и тот же элемент .

Примеры:

1.   где , +₁₀ – сложение по модулю 10. Тогда  - гомоморфизм из А в В.

Изоморфизм – гомоморфизм, который является биекцией.

Теорема. Если  изоморфизм, то  тоже изоморфизм.

Доказательство: Рассмотрим произвольную операцию j из сигнатуры А и соответствующей ей yиз В, тогда, так как f- гомоморфизм,   и кроме того ранее доказана теорема, что если f - биекция. Следовательно существует f ^-1 . Обозначим f(a_i) = b_i тогда равенство приобретает вид

f ^–1 (b_i) = a_i.   f^-1(y (b₁,....,b_n))=f ^–1 (y (f (a₁)...f(a_n)) = f^-1 (f(j(a₁...a_n))) = j(a₁...a_n) = y(f^-1(b_i)... f^-1(b_n)).

Окончательно f^-1(y(b₁,....,b_n)) = j(f^-1(b_i)... f^-1(b_n)). Следовательно обратное отображение тоже изоморфизм.

Алгебраические структуры принято рассматривать с точностью до изоморфизма, т.е. рассматривать классы эквивалентности по отношению изоморфизма.

Полугруппой  называется алгебра с одной ассоциативной бинарной операцией.

Пример: Х = { a | aє R ; a > 0 }        < X; * > и < X;+ >  - ­полугруппы с заданной на

 нем операцией  а    b = a^b   не будет полугруппой, т.к.  не всегда  (а     b)   c = a  (b   c)

               Нейтральным элементом называется а₀ такой что для      а є А  а₀     а = а    а₀ = а.

 При сложении чисел это 0 , при умножении 1.

 Но не для всех полугрупп  а₀ существует  Х = {n| n = 2k; n є N} для < X;+ >  и < X; * >

 отсутствует нейтральный элемент .

         Если А – полугруппа и е – её нейтральный элемент, то говорят, что а обратен к b.

 если  а    b = b    a = e.

               Например. 1.  если операция * => a ^–1 = e

2.  если операция + => -a = e

Моноид – полугруппа с единицей.

               Группа – это алгебра с одной бинарной ассоциативной операцией, с нейт –

ральным элементом и обратна (для       а є А        а ^–1  є А).

               Или полугруппа с единицей и обратными элементами называется группой.

               Или моноид с обратными элементами.

Пример 1) Х = { 1;-1 }, то  <X; * > - группа т.к. * - ассоциативная биективная операция

1 = е, (1) ^–1  = 1; (1) ^–1  = -1

2.    M – множество невырожденных квадратных матриц <M ;   > - группа. Е – еденич – ный элемент. Обратный элемент – М ^–1  

3)  <Z; +> и <R⁺ ; *>

Примеры полугрупп:

4) Сложение векторов образует группу по сложению.

       

                                                     ассоциативность

 - нулевой вектор – а₀ – единичный элемент  обратный элемент – а ^–1 = - . т.к.

5)                                  Повороты правильного треугольника вокруг его центра в одном

             В                                      направлении.

                                                        а₀ = 0^о + 360^о * n

    А                С                a₁ = 120^o + 360^o * n

                                          a₂ = 240^o + 360^o * n

        и

3. Если группа обладает свойством,   а     b = b     a  то она называется коммутативной

или Абелевой.

               Кольцо – это алгебра с двумя бинарными операциями       и      (“сложение” и

“умножение”) в которой выполняются => свойства:

1. сложение ассоциативностей

2.

3. ;  обратный элемент коммутативности по сложению

4.

5.умножение ассоциативностей

6.умножение дистрибутивно слева и справа.

Или иначе Кольцо – это множество М с двумя бинарными операциями , где

               - Абелева группа по Сложению и полугруппа по умножению, где операция дистрибутивна справа и слева.

               Кольцо называется коммутативным если выполненакоммутативность

по умножению.

               Кольцо называется кольцом с единицей если , т.что .

Элементы кольца (а) называются левым(правым) делителем нуля если:, но

т.ч.  , но a * b = 0, (b * a = 0)  например матрицы фиксированной размерно -

ти 

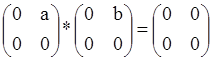
Пример 1. все квадратные матрицы порядка n с действительными элементами образу –

ют кольцо относительно операций сложения к умножению матриц.(Кольцо не ком –

мутативно, но с единицей. )

2. Алгебра коммутативное кольцо с единицей
3. Алгебра  коммутативное кольцо с единицей
4. не группа, т.к.

ПОНЯТИЯ АЛГЕБРЫ ЛОГИКИ

Функции , где  называются функциями алгебры логики или Булевыми функциями.

Множество всех булевых функций от  n  переменных можно обозначить .

Булеву функцию от  n  переменных можно задать таблицей истинности.

х1, х2, … , хn	f(х1, х2, … , хn)
0 … 0 0
0 … 0 1
0 … 1 0
… …
1 … 1 1

ТЕОРЕМА (без доказательства)

Если число переменных  n, то в таблице истинности имеется   строк,  соответствующих всем различным комбинациям значений переменных,  которым можно поставить в соответствие   различных столбцов значений функции. 

х	f1(х)	f2(х)	f3(х)	f4(х)
0	0	0	1	1
1	1	0	1	0

Пример:  При n=1. 

f₁ – тождественная функция (переменная);

f₄ – отрицание переменной;

f₁ – константа «0»;

f₃ – константа «1».