4.
строятся расчетные схемы вала. В любом редукторе силы (F,
F , Fа, Fк и т.д.) действуют в двух
взаимно-перпендикулярных плоскостях, поэтому расчётные схемы строятся в
горизонтальной (Г) и фронтальной (Ф) плоскостях. Действующие на вал нагрузки
наносятся с учётом направления их действия (рис.1,2,3). Расчётные схемы для
валов (ведущего и ведомого) цилиндрического редуктора и ведомого вала
червячного редуктора представлены на рис.8. на рис.9 и 10 показаны расчётные
схемы для расчёта, ведущего и ведомого валов конического редуктора, а на рис.11
– вала червяка. Для удобства дальнейших расчётов рекомендуется расчётные схемы
совмещать с эпюрами изгибающих крутящих моментов (рис.8). На всех расчётных
схемах присутствует изгибающий момент m,
который возникает от действия осевых усилий Fа
(следовательно, m не будет только на расчётных схемах валов прямозубых шевронных цилиндрических редукторов).
Величина этого момента определяется следующим образом:
m = Fа * (d1/2) – для ведущего вала цилиндрич. редуктора;
m = Fа * (d2/2) – для ведомого вала цилиндрич. редуктора;
m = Fа1 *(dа/2) - для ведущего вала конического редуктора;
m = Fа2 * (dc2/2) – для ведомого вала коническ. редуктора;
m = Fа1 * (d1/2) – для вала червяка;
m = Fа2 * (d2/2) – для вала червячного колеса.
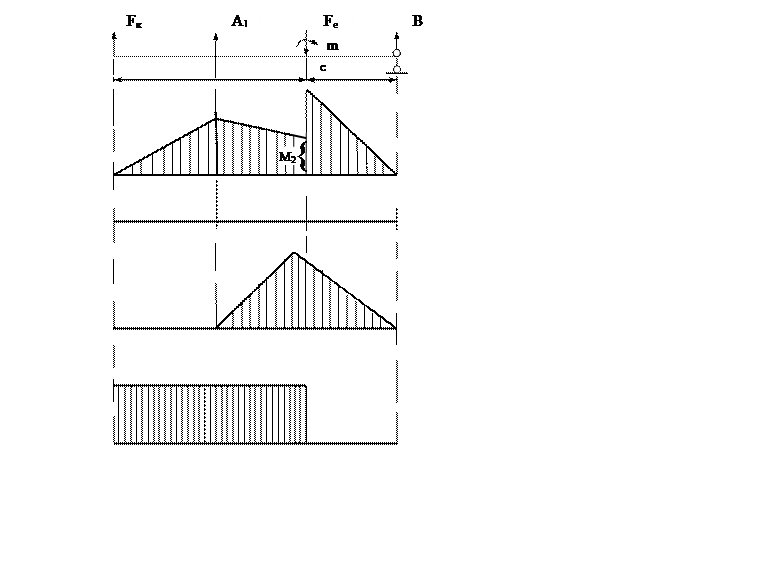
Рис.8 расчетная схема
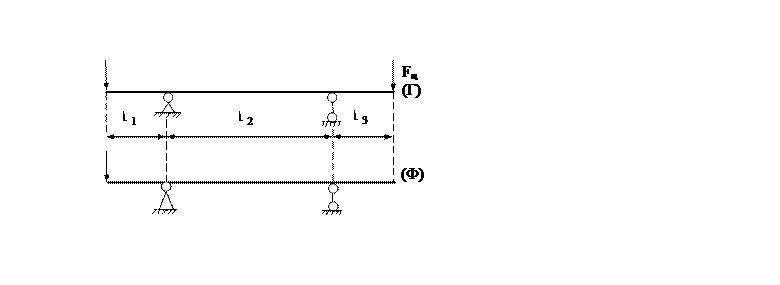
Рис.9
Расчётная схема.
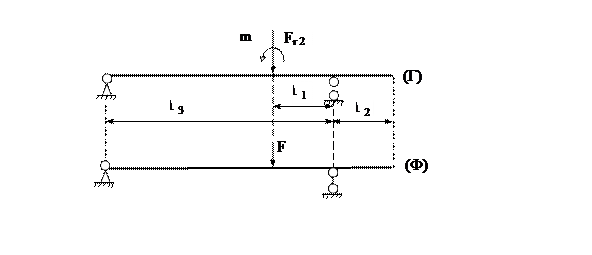
Рис.10
Расчётная схема.
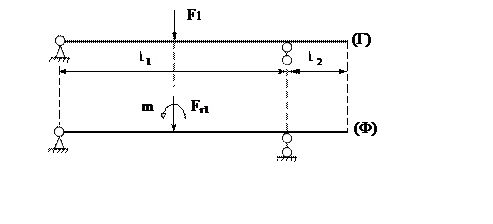
Рис.11. Расчётная схема.
Следовательно, для нашего примера
m = Fa * d1/2 = 0.7 * 103 * 50 Нмм.
5. Строятся эпюры изгибающих (в горизонтальной Мг и фронтальной Мф плоскостях) и крутящих моментов (рис.8). Обозначи опорные реакции А1, А2, В1, В2 и определим их.
Σ Fy = А1 + В1 + Fк - Fr =0 ; (1)
Σmоmа = Fк ﺎ 1 + Fr * 0.5ﺎ 2 + m – b1ﺎ 2 = 0 ; (2)
Из (2) получаем:
В1 = (Fr * 0.5 ﺎ 2 + m + Fkﺎ 1) / ﺎ 2 = ( 1.5*103*0.5*80+35*103*60)/ 80 = 1.95*103 Н.
Из (1) имеем:
А1 = - Fк +Fr –B1= -103+1.5*103- 1.95*103 = -1.45*103 Н.
Очевидно,
А2 = В2 = F/2 = 4*103 / 2 = 2*103 Н.
Определяем изгибающие моменты в сечении А-А (рис.8)
М1 = Fk * ﺎ 1 = 103 * 60 = 60*103 Нмм;
В сечении С-С (рис.8 )
М2 = Fk ( ﺎ 1+ ﺎ 2/ 2) + A1* ﺎ 2 / 2 = 103 * 100 + ( -1.45 * 103 ) * 40 = 42 * 103 Нмм;
М3= А2 ﺎ 2 /2 = 2 * 103 * 40 = 80 * 103 Нмм;
М4 = В1ﺎ 1 / 2 = 1,95 * 103 * 40 = 78 * 103 Нмм.
6. Определяем диаметры участков вала. Рекомендуется вычислить минимальный и максимальный диаметры вала, а диаметры промежуточных ступеней выбирать между этими расчетными значениями. Так для рассматриваемого примера (рис.4) достаточно определить диаметры d 1 и d2 . При выборе диаметров посадочных мест под подшипники стоит иметь ввиду, что подшипники качения ( начиная с d = 20 мм) имеют внутренний диаметр, оканчивающийся на цифры 5 или 0.
На участках вала диаметром d1 действуют максимальный изгибающий момент в горизонтальной плоскости М1 = 60 * 103 Нмм (рис.8) и крутящий момент Т1 = 2 * 105 Нмм. Изгибающего момента в фронтальной плоскости нет.
Определяем приведенный момент
 |
|||
 |
|||
|
Мпр.а = =
Уравнение прочности
σи = .Мпр.а / Wx ≤ [σ], где Wx – линейный момент сопротивления сечения Wx = πd13 /32
[ σ ] – допускае6мое напряжение для материала вала. Обычно, принимают
[ σ ] ≈ 0,2σв = 0,2 * 570 ≈ 110 Н/мм.
Имеем:
32Мпр.а / πd13 ≤ [σ],
|
откуда
|
d1
≥ = = 25
мм.
Если выходной конец вала работает на чистое кручение (валы червячных редукторов, ведомые валы других типов редукторов), то диаметр определяют из условия прочности на кручение
d1≥ 
, где Т – крутящий момент на рассчитываемом валу;
[ τ ]кр – допускаемое напряжение на кручение для материала вала
[ τ ]кр ≈ 0,15σв.
На участке диаметром d4 (рис.8) в горизонтальной плоскости действует максимальный изгибающий момент М4 = 78 * 103 Нмм, в фронтальной плоскости - М3 = 80 * 103 Нмм и крутящий момент Т1 = 2 * 105 Нмм. Определяемрезультирующий изгибающий момент
Мрез.с = 
Приведенный момент
Мпр.с = 
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.