нашей задаче (т + n - 1) =3 + 4 - 1 - 6, где т - 3, - количество поставщиков, n = 4, - количество потребителей. Заполненных клеток в табл. 9 также оказалось 6. Следовательно, план невырожденный.
Замечание. Если план окажется вырожденным, т.е. заполненных клеток будет меньше, чем 6, то их количество нужно довести до 6, внося в некоторые пустые клетки нулевые поставки. Нулевую поставку желательно вписывать в клетку с наименьшим тарифом, но при этом обязательно так, чтобы она не образовала с ранее заполненным клетками замкнутого цикла (понятие «цикл» рассмотрено ниже). В результате заполненных клеток должно оказаться ровно (т + п - 1).
Стоимость перевозок, соответствующая первому опорному плану, определяется с помощью тарифов, стоимость груза 1 руб./т.км.
С= 14∙12+9∙7+9∙14+21∙15+11∙21+14∙22=1211 руб., где С – полная стоимость перевозок, руб.
2. Введем вспомогательные величины, называемые потенциалами: αi - потенциалы поставщиков (строк); βj - потенциалы потребителей (столбцов).
Потенциалы вычисляются для заполненных клеток из условия:
αi+βj=Cij , где Cij – тарифы этих клеток в задаче.
α1+β1=12; α1+β3=7; α1+β4=14; α2+β2=15; α3+β2=21; α3+β4=22;
Значение одного из потенциалов выбираем произвольно. Например, α1 = 0. Тогда значения остальных потенциалов легко найдутся из указанной системы:
α2=2; α3=8; β1=12; β2=13; β3= 7; β4=14;
Эти значения потенциалов проставим в табл. 9 в столбец поставщиков и в строку потребителей. Получим табл. 10 следующего вида:
Таблица 10.
|
Пункт |
Магазин №12 β1=12 |
ТЦ №3 β2=13 |
Магазин №8 β3=7 |
ТЦ №5 β4=14 |
Запасы |
|
Молкомбинат №1 α1=0 |
12 14(-) |
20 - |
7 9 |
14 9(+) |
32 |
|
Молкомбинат №3 α2=2 |
7 -(+) ? |
15 21(-) |
12 - |
19 - |
21 |
|
Молкомбинат №4 α3=8 |
29 - |
21 11(+) |
30 - |
22 14(-) |
25 |
|
Потребности |
14 |
32 |
9 |
23 |
78 |
3. Проверим план на оптимальность. Оптимальный план должен удовлетворять условию для всех пустых клеток:
αi+βj≤Cij
Проверяем пустые клетки:
Клетка (1,2) 0+13≤20
Клетка (2,1) 2+12≥7
Клетка (2,3) 2+7 ≤12
Клетка (2,4) 2+14≤19
Клетка (3,1) 8+12≤29
Клетка (3,3) 8+7≤30
Как показывают вычисления, для клетки (2,1) условие оптимальности не выполняется. Следовательно, план не является оптимальным и его нужно улучшать. Для этого загружаем «неоптимальную» клетку (2,1) за счет перераспределения груза в других клетках.
Для того чтобы осуществить перераспределение груза, построим цикл перерасчета к «неоптимальной» клетке. Здесь циклом называется многоугольник, у которого:
1) все стороны лежат в строках и столбцах;
2) все углы прямые;
3) все вершины лежат в заполненных клетках, а одна вершина - в свободной неоптимальной клетке;
4) в цикл включены лишь те клетки, где находятся его вершины. Циклы перерасчета могут иметь следующую форму (рис. 1).
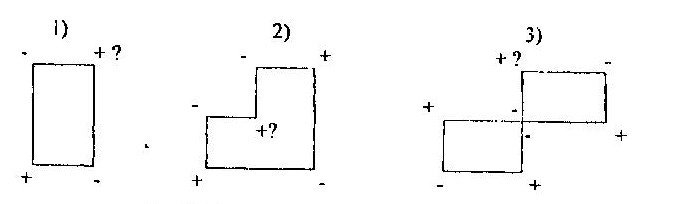
Рис. 1. Примеры основных видов циклов
Число их вершин обязательно четно. «Неоптимальная» клетка может находиться в любой вершине цикла. Для определенности «неоптимальная» клетка каждого цикла отмечена вопросом.
По циклу будем перемешать поставку. Для нахождения величины этой поставки сначала проставим знаки в вершине цикла: в «неоптимальную» клетку ставим знак «+», а далее, совершая обход по циклу, чередуем знаки «-» (минус) и «+» (плюс) в его вершинах. Из клеток, отмеченных знаком «-» (минус), выбираем наименьшую поставку.
Наименьшая из поставок, отмеченных знаком «-», равна 14. Перемещаем ее по циклу. При этом прибавляем по 14 единиц к поставкам, находящимся в вершинах со знаком «+», и вычитаем по 14 единиц из поставок, находящихся в вершинах со знаком «-», В результате всех этих перемещений приходим к новому плану, указанному в табл. 11.
Таблица 11.
|
Пункт |
Магазин №12 β1=12 |
ТЦ №3 β2=20 |
Магазин №8 β3=7 |
ТЦ №5 β4=14 |
Запасы |
|
Молкомбинат №1 α1=0 |
12 0 |
20 - |
7 9 |
14 23 |
32 |
|
Молкомбинат №3 α2= -5 |
7 14 |
15 7 |
12 - |
19 - |
21 |
|
Молкомбинат №4 α3=1 |
29 - |
21 25 |
30 - |
22 - |
25 |
|
Потребности |
14 |
32 |
9 |
23 |
78 |
Этот план получился вырожденный, поскольку в нем:
1) соблюдены балансы по всем строкам и столбцам;
2) число заполненных клеток равно: т + п - 1 = 5;
3) из заполненных клеток (или их части) нельзя образовать ни одного замкнутого цикла.
Так как план оказался вырожденный, нам необходимо ввести нулевую поставку, чтобы выполнялось условие т + п - 1 = 6. нулевую поставку желательно вписывать в клетку с наименьшим тарифом, но при этом обязательно так, чтобы она не образовывала с ранее заполненными клетками замкнутого цикла.
Стоимость перевозок, соответствующая второму опорному плану.
С= 0∙12+9∙7+23∙14+14∙7+7∙15+25∙21=1113 руб., где С – полная стоимость перевозок, руб.
Выясним, оптимален ли полученный план, повторив весь ход рассуждений с помощью метода потенциалов начиная с п. 2.
α1+β1=12; α1+β3=7; α1+β4=14; α2+β1=7; α2+β2=15; α3+β2=21;
Полагая α1 = 0, получим значения остальных потенциалов:
α2= -5; α3=1; β1=12; β2=20; β3=7; β4=14;
αi+βj≤Cij
Проверяем пустые клетки:
Клетка (1,2) 0+13≤20
Клетка (2,3) 2+7≤12
Клетка (2,4) 2+14 ≤19
Клетка (3,1) +12≤29
Клетка (3,3) 8+7≤30
Клетка (3,4) 8+14=22
Все клетки оптимальны, значит, полученный в табл. 11. план, оптимален.
Ответ: оптимальный план перевозок: Х11=0; Х13=9; Х14=23; Х21=14; Х22=7; Х31=25. Расходы по его осуществлению минимальны и составляют С=1113 руб.
Министерство образования и науки Российской Федерации
Федеральное Агентство по Образованию
Государственное Образовательное Учреждение Высшего
Профессионального Образования
Новосибирский Государственный Технический Университет

Кафедра ТМС
Расчетно-графическая работа
«Организация грузовых перевозок»
Вариант 6.
Выполнил: Комаров А. А.
Факультет: МТ
Группа: ТА – 502
Принял: Рахимянов К.Х.
Новосибирск 2009
Продовольственные грузы

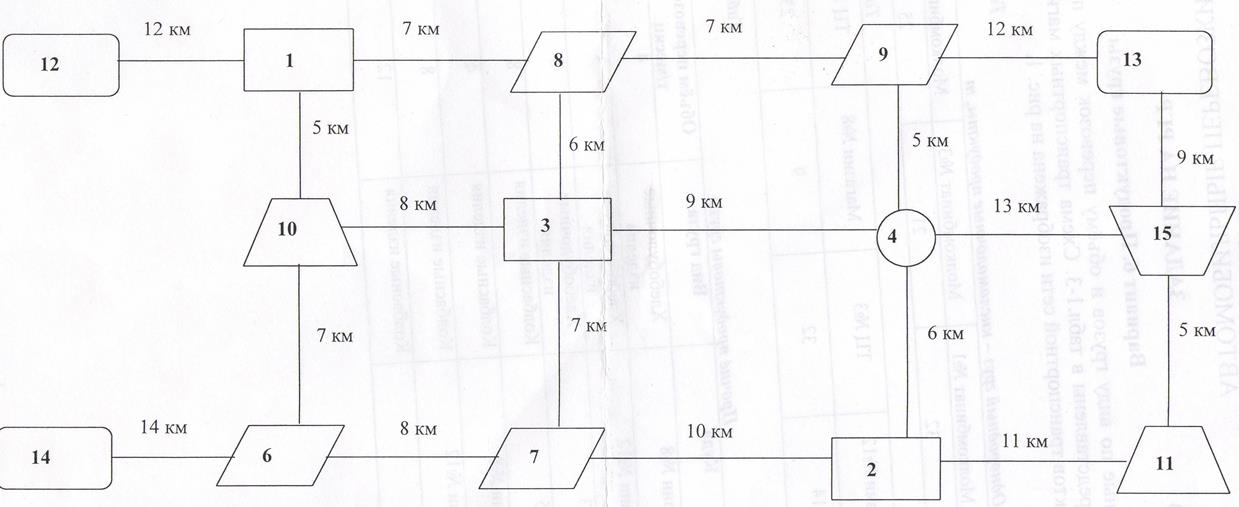
Объекты: 1 – Молкомбинат №1; 2 – Хлебозавод №3; 3 – Хлебозавод №4; 4 – транспортная развязка; 6 – магазин №12;
7 – ТЦ №3; 8 – магазин №8; 9 – ТЦ №5; 10 – Молкомбинат №3; 11 – Молкомбинат №4; 12 – Мясомолочный
комбинат №2; 13 - Мясомолочный комбинат №4; 14 - Мясомолочный комбинат
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.