Термический
КПД цикла с подводом тепла V=const
зависит только от степени сжатия, причем,чем больше e
, тем выше КПД. Так для воздуха при e=4, 
= 0.38, а при e=10
=0.55.
С этой точки зрения увеличение общей степени сжатия можно осуществить до двигателя в специальном компрессоре и увеличить термический КПД. Этот вывод справедлив для всех ДВС.
Реально в карбюраторных двигателях степень сжатия не превышает 12, так как при больших значениях происходит самовоспламенение смеси. Этот-процесс носит детонационный характер и приводит к разрушению конструкции двигателя. Каждый вид топлива имеет свои антидетонационные свойства, характеризующиеся октановым числом.
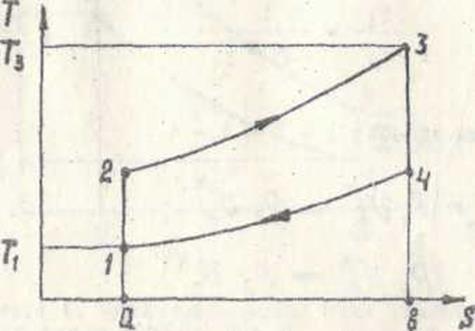
Рис. 4.5. Т-Sдиаграмма двигателя с подводом теплоты при V=const.
Рассматриваемый цикл в Т-S диаграмме показан на рис. 4.5. Подводимое тепло q1 на диаграмме изображается площадью а-2-3-b–a , отводимое тепло q2 - площадью a-1-4-b–a, а тепло, превращаемое в работу, - площадью 1-2-3-4-1.
4.2.2. Цикл Дизеля (P=const)
Для повышения степени сжатия целесообразно сжимать в цилиндре только воздух, а потом впрыскивать в него топливо. На этом принципе основан цикл Дизеля. Индикаторная диаграмма такого двигателя показана на рис. 4.6. В процессе а-1 в цилиндр всасывается чистый воздух, в процессе 1-2 осуществляется его сжатие. В начале обратного хода поршня в цилиндр впрыскивается топливо и за счет высокой температуры сжатого воздуха (степень сжатия в этих двигателях достигает 15-24) происходит его воспламенение. Так как сгорание происходит в процессе расширения, процесс протекает при постоянном давлении (процесс 2-3).
После сгорания топлива процесс расширения протекает адиабатным, в точке 4 открывается клапан выхлопа и давление снижается по изохоре 4-5. Далее газ выбрасывается из цилиндра в атмосферу и цикл повторяется.
Также как и в предыдущем случае, индикаторную диаграмму цикла Дизеля заменим идеализированным циклом, термодинамически эквивалентным индикаторному (рис. 4.7). Этот цикл состоит из двух адиабат 1-2 и 3-4, изобары 2-3, по которой осуществляется подвод тепла q1 и изохоры 4-1, по которой осуществляется отвод тепла q2.
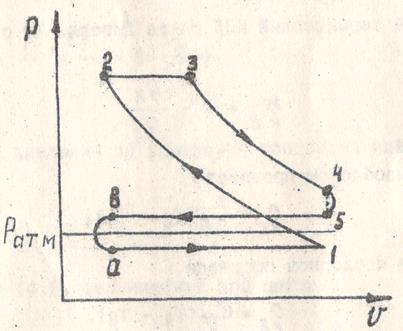
Рис. 4.6. Индикаторная диаграмма цикла Дизеля.
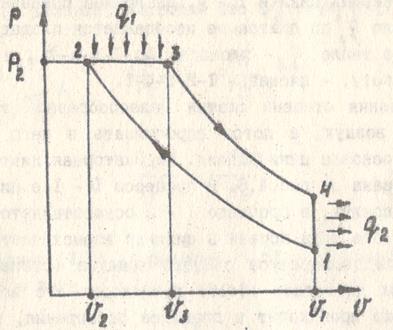
Рис. 4.7. Идеализированный цикл Дизеля.
Определим термический КПД цикла Дизеля. Из общего выражения для КПД
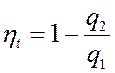(4.10)
Теплота q1 в изобарном процессе
,
(4.11)
где CP – теплоемкость газа в процессе при P=const.
Теплота q2 в изохорном процессе
(4.12)
С учетом этого термический КПД
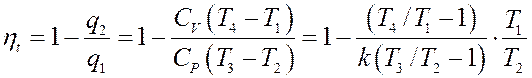, (4.13)
где k=CP/CV – показатель адиабаты.
В изобарном процессе идеального газа
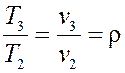. (4.14)
Здесь r – степень предварительного расширения воздуха. Запишем уравнения адиабат 1-2 и 3-4
; 
(4.15)
после
почленного деления, учитывая что 
и 
получаем
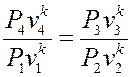или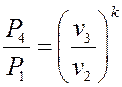 
(4.16)
Заменим отношение давлений из уравнения состояния идеального газа
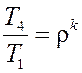. (4.17)
С учетом (4.17) и (4.6) выражения
для определения термического КПД цикла Дизеля имеет вид
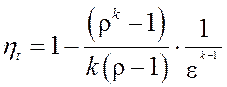. (4.18)
Из (4.18) следует, что термический КПД цикла Дизеля тем больше, чем больше степень сжатия e и чем меньше степень предварительного расширения r. Так при степени сжатия e=15 уменьшение r от 2.5 до 1.6 увеличивает КПД с 0.53 до 0.57, при степени сжатия e=20 уменьшение r от 2.5 до 1.6 увеличивает КПД с 0.63 до 0.73.
В Т-S диаграмме цикл Дизеля показан на рис. 4.8. Подводимая теплота q1, изображается площадью а-1-2-3-b–a, отводимая теплота q2, площадью a-1-4-b–a, работа цикла равна площади 1-2-3-4-1.
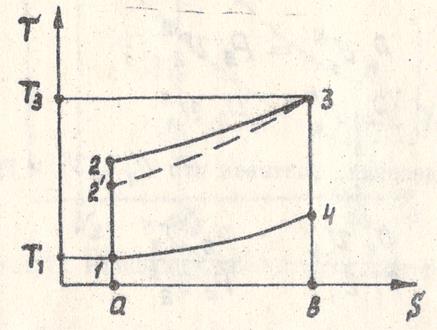
Рис. 4.8. Цикл Дизеля в Т-S координатах.
Для сравнения на Т-S диаграмме изображен цикл Отто при сравнимых условиях, т.е. одинаковых параметрах P1 и T1, температуре Т3 и степени сжатия e. Здесь 2-3 это изобара рабочего хода цикла Дизеля, а 2-3 изохора рабочего хода цикла Отто. Так как для идеальных газов CP>CV, следовательно,
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.