Проектирование привода моечного барабана (мощность на валу барабана - 6 кВт, срок службы привода - 0,5 лет)

Конические передачи сложнее цилиндрических в изготовлении и монтаже. Наиболее употребительным диапазоном передаточных отношений можно считать .

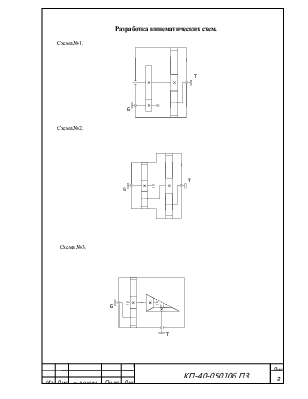
1. Кинематический расчет привода.

1.1 Зная синхронные скорости вращения двигателя n_двj, определяем возможное передаточное отношение. Результаты расчета представлены в табл. 1:

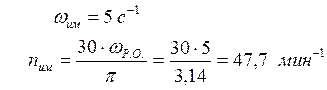
1.2 Принимаем значение передаточного отношения  открытой передачи: i_оп=5

1.3 Определяем возможное передаточное отношение редуктора. Результаты расчетов сведены в табл. 1:

                                                        Кинематический расчет привода.                                                               Табл. 1

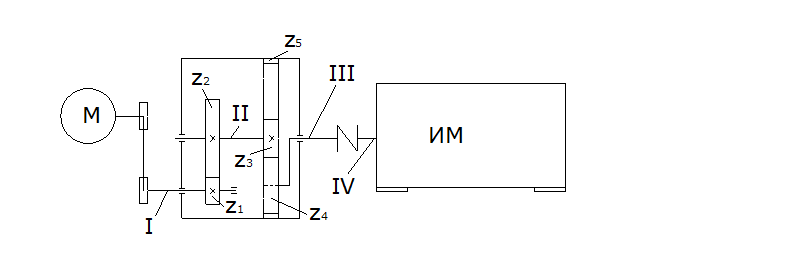
1.4 Принимаем к исполнению вариант “1”. Для планетарно-цилиндрического двухступенчатого редуктора наиболее рациональным оказывается передаточное отношение u_р=12,58, которое обеспечивается электродвигателем  с синхронной частотой вращения n_дв.=3000 мин^-1 (табл. 1).

1.5 Определяем КПД привода, принимая значение КПД отдельных передач:

h_муфт=0,98 – КПД муфты;

h_оп =0,95 – КПД открытой передачи;

h_тих=0,95 – КПД тихоходной ступени;

h_быстр=0,98 – КПД быстроходной ступени;

h_общ.= h_муфтh_опh_тихh_быстр =0,98·0,95×0,95·0,98=0,867

1.6 Находим расчетную мощность  и угловую скорость двигателя:

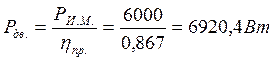
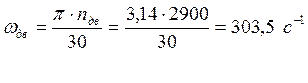
    1.7 По справочнику подбираем двигатель112М2/2900, номинальную частоту вращения 2900  мин^-1 .

  1.8 Уточняем передаточное отношение привода:

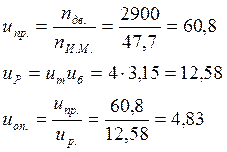
1.9 Определяем частоту вращения, угловую скорость и мощность всех валов:

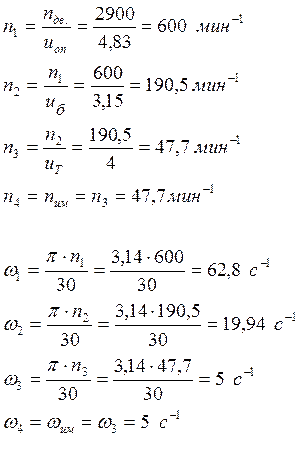
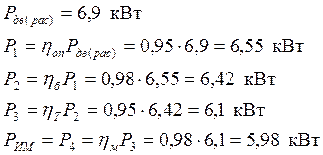
1.10 Определение крутящих моментов на валах:

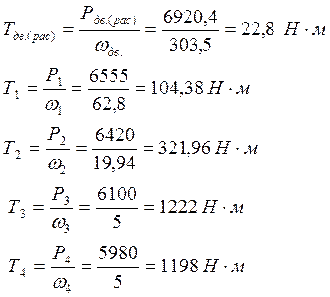
2. Расчёт зубчатых колёс редуктора

2.1. Выбор материала для зубчатых колес

Так как  в техническом задании нет особых требований к габаритам передачи, выбираем материал со средними механическими характеристиками: сталь 40Х, термообработка – улучшение, твердость быстроходная ступень для шестерни НВ 260

для колеса НВ 240;

тихоходная ступень   для солнечного и колокольного колес НВ 260

для сателлита НВ 240;

2.2. Расчет допускаемых контактных напряжений [s_H]

Цилиндрическая передача

Допускаемое контактное напряжение определим по формуле:

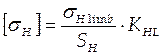, где  S_H  - коэффициент безопасности  (при  улучшении  S_H =1,1);

 - предел контактной выносливости, соответствующий базовому числу циклов

(при НВ £ 350    );

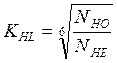- коэффициент долговечности, учитывающий влияние срока службы и ре  жима нагрузки;

N_HO - базовое число циклов;

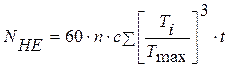 - эквивалентное число циклов;

n – частота вращения вала, с =1 –  число зацеплений,

T_i – текущий крутящий момент,

T_max – максимальный крутящий момент за цикл (взяты из графика загрузки барабана),

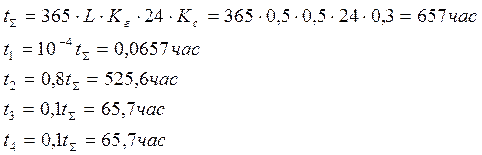
- суммарное время работы передачи где   L – срок службы, год

К_г- коэффициент годового использования,

К_с - коэффициент суточного использования.

Для шестерни:

МПа;

N_HO =  циклов;

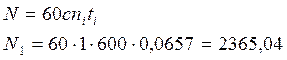                                               - число циклов при Tmax  (N>)

   условие выполнилось, т.о. Tmax=Tном

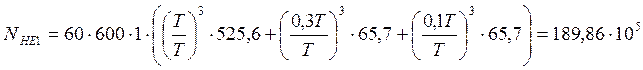циклов;      ;

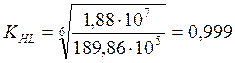
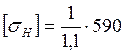 =536,36 МПа.

Для колеса:

МПа;

N_HO =  циклов;

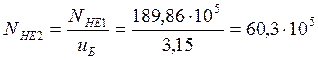циклов;

     ;

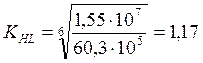
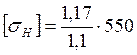 = 585 МПа.

Для прямозубой передачи в расчёт принимаем МПа.

Планетарная  передача

Допускаемое контактное напряжение определим только для солнечного колеса, как более нагруженного, по формуле:

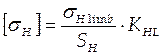, где  S_H  - коэффициент безопасности  (при  улучшении  S_H =1,1);

 - предел контактной выносливости, соответствующий базовому числу циклов

(при НВ £ 350    );

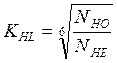  - коэффициент долговечности, учитывающий влияние срока службы и режима нагрузки;

N_HO -базовое число циклов;

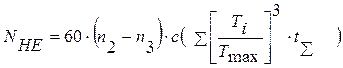 - эквивалентное число циклов;

n₂,n₃ – частоты вращения промежуточного и выходного валов соответственно, с =1 –  число зацеплений,

T_i – текущий крутящий момент,

T_max – максимальный крутящий момент за цикл (взяты из графика загрузки барабана),

t_∑- суммарное время работы передачи

Для солнечного колеса:

МПа;

N_HO =  циклов;

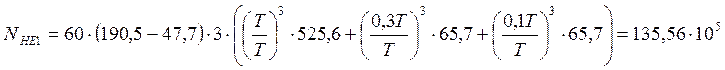циклов;      ;

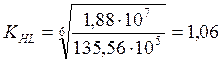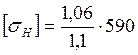 =566,4 МПа.

2.3. Расчет допускаемых напряжений изгиба [s_F]

Цилиндрическая передача

Допускаемые напряжения изгиба зубьев при расчёте на усталостную прочность определим из приведённого ниже соотношения:

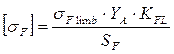, где - предел выносливости при изгибе (),

Y_A – коэффициент, учитывающий характер приложения нагрузки (если передача нереверсивная, то Y_А = 1),

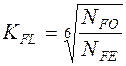– коэффициент долговечности,

N_FO=4 10⁶ – базовое число циклов,

N_FЕ =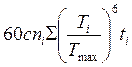 – эквивалентное число циклов,

S_F – коэффициент безопасности (S_F =1,65).

Для шестерни:

;

N_FЕ1=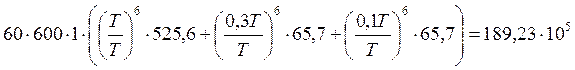циклов;

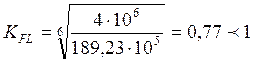
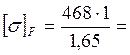283,63 МПа.

Для колеса:

N_FЕ2 = 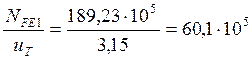циклов;

;          

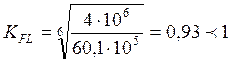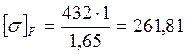МПа.

Планетарная передача

Допускаемые напряжения изгиба зубьев при расчёте на усталостную прочность определим только для солнечного колеса, как более нагруженного, из приведённого ниже соотношения:

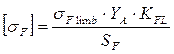, где - предел выносливости при изгибе (),

Y_A – коэффициент, учитывающий характер приложения нагрузки (если передача нереверсивная, то Y_А = 1),

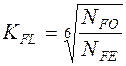– коэффициент долговечности,

N_FO=4 10⁶ – базовое число циклов,

N_FЕ =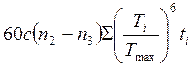 – эквивалентное число циклов,

S_F – коэффициент безопасности (S_F =1,65).

Для солнечного колеса:

;

N_FЕ1=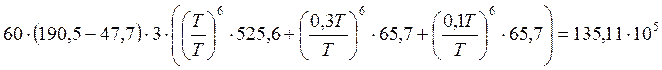циклов;

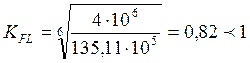
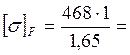337,3 МПа.

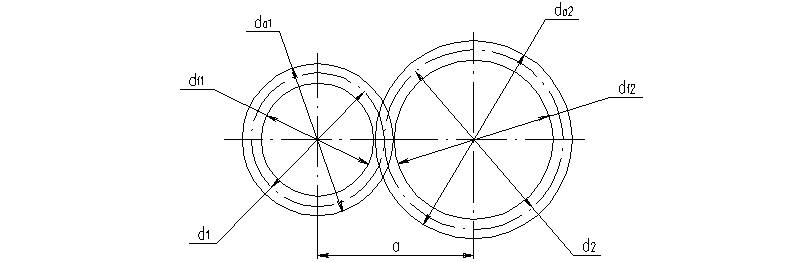
4.  Расчет геометрических параметров быстроходной прямозубой ступени.

Межосевое расстояние найдем по формуле:

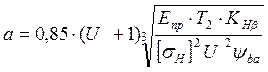, [1, с.135]

где U  = 3,15 – передаточное отношение ступени;

Е_пр = 2,1×10⁵ МПа – модуль упругости;

Т₂ = 321,96 Н×м – момент на валу с колесом данной ступени;

        = 536,36 МПа – наименьшее допускаемой контактное напряжение ступени;

y_ba = 0,4– коэффициент ширины венца [1, табл.8.4].

К_Нb = 1,05 – коэффициент неравномерности распределения нагрузки по длине контактной линии [1, рис.8.15];

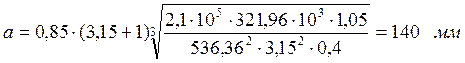
Принимаем , тогда модуль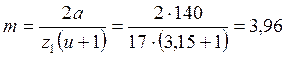

Принимаем по стандарту  m = 4

Предварительный расчет делительных диаметров:

Число зубьев колеса: ,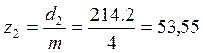

Принимаем число зубьев колеса , тогда  

Пересчитаем межосевое расстояние:

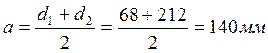
Рассчитаем основные геометрические параметры передачи:

Делительные диаметры:

.

Диаметры вершин:

.

Диаметры впадин:

Ширина венца колеса:

.

Ширина шестерни: .

4. Расчет геометрических параметров тихоходной прямозубой ступени.

Принимаем , число сателлитов с=3, тогда

Проверим правильность подбора по условиям:

-соосности

           21+21=63-21

-сборки

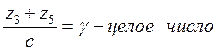
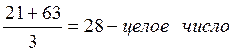
-соседства

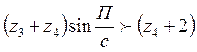
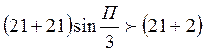
Условия выполняются.

Внешний делительный диаметр  солнечного колеса:

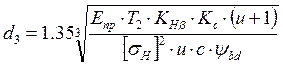, где U  = 4 – передаточное отношение ступени;

Е_пр = 2,1×10⁵ МПа – модуль упругости;

Т₂ = 321,96 Н×м – момент на валу с колесом данной ступени;

= 566,4  МПа – наименьшее допускаемой контактное напряжение ступени;

К_с=1,15- коэффициент, учитывающий неравномерность нагрузки между