*****
Vb - коэффициент, учитывающий наклон зуба конической передачи,
b=00 - Vb=1 - для прямозубой конической передачи; нарисовать
b=150 - Vb=1,22 - для косозубой конической передачи; нарисовать
b=350 - Vb=1,5 - для конической передачи с круговыми зубьями;
из диаметра шестерни находим диаметр колеса
![]()
теперь можно ориентировочно определить ширину колеса
ширина венца зубчатого колеса ![]()
ширина шестерни ![]()
ширина венца конического колеса ![]() нарисовать
нарисовать
внешнее конусное расстояние конических передач
![]() нарисовать
нарисовать
вычислить углы делительных конусов
![]()
![]()
определить предварительно диаметры валов db редуктора по формуле
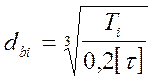
где: Ti - крутящий момент на соответствующей шестерни/колесу;
[t] - пониженное допускаемое напряжение для материала вала принимают [t]=20¸30 Мпа
вычерчивают в масштабе 1:2 полученные шестерни и колёса
Лекция 6.
17. Допускаемые предельные напряжения при перегрузках.
Рассмотренные выше формулы для расчёта напряжений в зубьях и допустимые напряжения рассматривались для штатных режимов работы редуктора, по циклограмме, по которой определялся режим долговечности, когда каждый режим нагрузки имеет определённую продолжительность по времени. Тем не менее, в режиме могут быть мгновенные перегрузки. В этом случае величины этих предельных напряжений сравниваются с предельными допустимыми напряжениями. Для контактных напряжений:
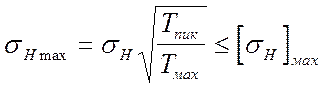 (1)
(1)
где: sH - напряжение, рассчитанное выше для штатного режима нагрузки;
Tmax - максимальное напряжение в штатном режиме нагрузки;
Tпик - пиковое кратковременное напряжение;
Допустимые напряжения рассчитываются для незакалённых или для объёмной закалки
![]()
где: sT - напряжение текучести (из таблиц);
для колёс подвергнутых поверхностному упрочнению
![]()
Для изгибных напряжений:
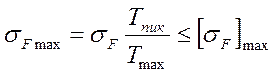 (2);
(2);
Допустимые напряжения для предельных изгибных напряжений
![]() для сталей HBЈ350;
для сталей HBЈ350;
![]() для сталей HBі350;
для сталей HBі350;
Особенности расчёта косозубых и шевронных цилиндрических передач.
Влияние косозубого зацепления на форму зуба
Профиль косого зуба в нормальном сечении совпадает с профилем прямого зуба нарезают его теми же инструментами, что и прямой зуб при этом происходит очевидное увеличение шага и модуля при торцевом взгляде на колесо
![]() - окружной шаг; (3);
- окружной шаг; (3);
![]() - окружной модуль; (4);
- окружной модуль; (4);
![]() - делительный диаметр (5);
- делительный диаметр (5);
где : b - угол расположения зуба;
n - индекс в нормальном к зубу сечении;
t - индекс в торцевом к колесу сечении.
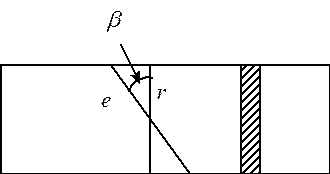
Форму косого зуба в нормальном сечении принято определять через параметры эквивалентного прямозубого колеса.
Если мы проведём плоскость нормальную к зубу , то она рассечёт цилиндрическое колесо с сечением в виде эллипса

здесь ![]()
форма зуба в сечении как мы указали выше, соответствует форме зуба прямозубого колеса, но с другим радиусом кривизны.
Радиус кривизны эллипса здесь на рисунке с=r
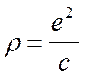
принимая радиус кривизны эллипса равным радиусу эквивалентного прямозубого колеса и подставляя значения e и c получим
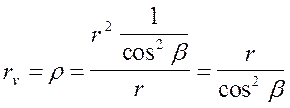 ;
; 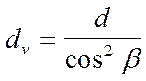 (6);
(6);
число зубьев
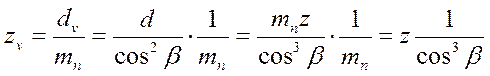 (7);
(7);
при том же физическом
размере колеса d эквивалентный радиус цилиндрического колеса больше реального физического
в 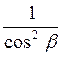 раз при число зубьев больше в
раз при число зубьев больше в ![]() раз.
раз.
Кроме того, если для прямого зуба существует торцевой коэффициент перекрытия, при этом переход с однозубого зацепления на двузубое происходит мгновенно, то в косозубом число зубьев в зацеплении всегда больше единицы
Сравнение торцевого перекрытия для прямозубого зацепления и осевого перекрытия для косозубого зацепления
напомним: для прямозубого зацепления коэффициент торцевого перекрытия равен
![]() (8);
(8);
где: ga - длина активной линии зацепления;
pb - шаг основной окружности

т.о. для прямозубого зацепления требовалось коэффициент торцевого перекрытия должен быть гарантированно больше единицы, для того, что бы не было разрыва в зацеплении
геометрические параметры косозубого зацепления
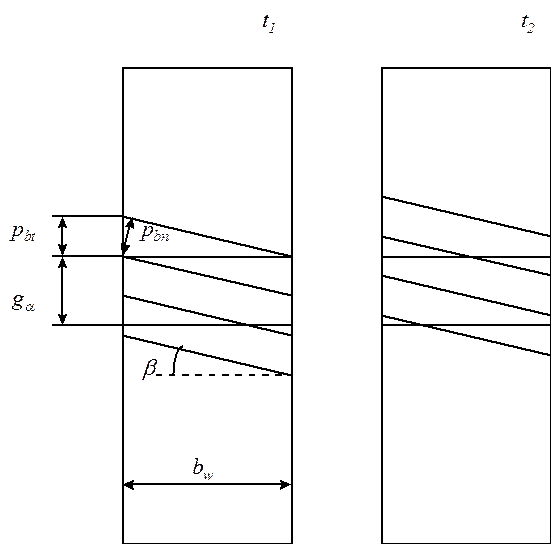
для косозубого зацепления формулируется коэффициент осевого перекрытия
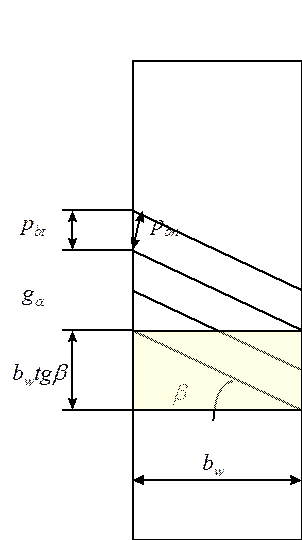
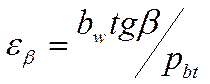 (9);
(9);
для косозубого зацепления длина активной линии зацепления может быть меньше шага зуба по основной окружности, но за счёт большего угла наклона зубьев в зацеплении всегда будет больше чем один зуб
длина одного зуба
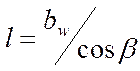 (10);
(10);
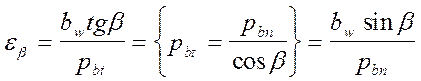 = >
= > 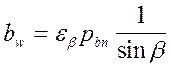 (11);
(11);
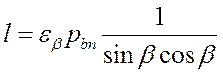 (12);
(12);
суммарная длина линии зацепления
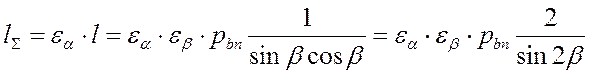
шаг зацепления
![]()
суммарная длина линии зацепления выраженная через модуль
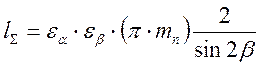
в реальных передачах b принимает значения 8ё200 для косозубых передач
для шевронных b принимает значения до 400
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.