



Лекция 4.
Продолжение лекции 3
расчётное значение a для нестандартных редукторов округляют к ряду:
от 40 до 130 через 5;
от 130 до 260 через 10;
от 260 до 420 через 20.
Для стандартных редукторов
1-й ряд - 40,50,63,80,100,125, 160, 200, 250,315,400 ...
2-й ряд - 140, 180,225, 280,335,450 ...
Стандартные значения yba :
0.1; 0.125; 0.16; 0.2; 0.25; 0.315; 0.4; 0.5; 0.63; 0.8; 1.0; 1.25.
Стандартные номинальные передаточные числа u
1-й ряд - 1.0; 1.25; 1.6; 2.0; 2.5; 3.15; 4.0; 6.3; 8.0;
2-й ряд - 1.12; 1.4; 1.8; 2.24; 2.8; 3.55; 4.5; 5.6; 7.1; 9.0; 11.2
Примерные соотношения между длиной зуба и модулем
зацепления 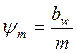
|
Конструкция |
|
|
Высоконагруженные и точные |
~30 |
|
Обычные передачи |
~20 |
|
Грубые и открытые передачи |
~10 |
10. Расчет прямозубой цилиндрической передачи на изгибную прочность.
Место максимальной концентрации напряжения - ножка.
Допущения:
1. Вся нагрузка передаётся через одну пару зубьев, от вершины зуба

такой режим реализуется для зубчатых передач, классом
7, 8 и ниже сила проведённая по линии зацепления проходит через
полюс зацепления под углом aw однако относительно данного зуба в данном положении
она находится под большим углом ![]()
показать на рисунке
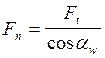 где
где 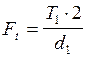 показать на рисунке
показать на рисунке
![]()
![]()
напряжение в ножке зуба располагается несимметрично, в силу того, что складывается из двух составляющих изгиба и сжатия, причём опасное сечение находится, согласно практики не в зоне максимального напряжения там где происходит сжатие а в зоне растяжения (согласно эмпирическим наблюдениям)
напряжение в опасном сечении можно рассчитать по формуле
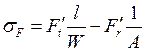 (7);
(7);
где: ![]()
![]() где
s - ширина ножки зуба показать на
рисунке l, bw,
s
где
s - ширина ножки зуба показать на
рисунке l, bw,
s
исходя из геометрического подобия зубьев вводят безразмерные коэффициенты
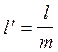
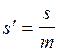
подставляя в (7) получим
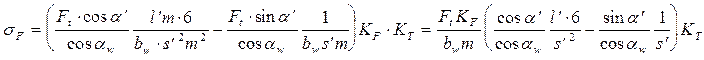
где:
KF - коэффициент расчётной нагрузки, KT - теоретический коэффициент концентрации напряжений обозначаем
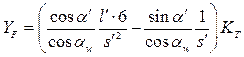 получим
получим
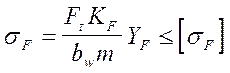 (8);
(8);
с учётом замены 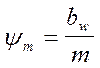
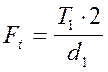 d1 =
mz1 получим
d1 =
mz1 получим
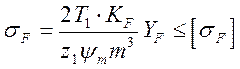 (9);
(9);
коэффициент расчётной нагрузки для изгиба КF=КFv×KFb подставляя, среднее приближённое значение(из таблиц) KFv = 1,5 и вычисляя m относительно sF получим расчётную формулу для определения модуля зубьев исходя из предельных изгибных напряжений
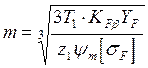 (10);
(10);
|
m |
1.0 |
1.25 |
1.5 |
1.75 |
2.0 |
2.25 |
2.5 |
3 |
3.5 |
4 |
4.5 |
5 |
5.5 |
6 |
7 |
8 |
9 |
|
2.75 |
3.25 |
3.75 |
Выбор модуля и числа зубьев (после расчёта на изгиб)
из формулы 4 напрямую следует, что величина контактных напряжений не зависит от модуля зубьев а зависит от диаметра делительной окружности d1 = mz1 а для изгибных напряжений модуль зубьев является критической величиной
41. Влияние числа зубьев и смещения при нарезании на форму и прочность зубьев.
Минимальное число зубьев нарезаемых без смещения равно 17 - граница подрезания, в этом случае диаметр начальной окружности будет равен диаметру делительной.
Показать форму зубьев z=18, z=25 смещение x=kx m отдаляет начальную окружность от центра при этом при сохранении числа зубьев происходит изменение их формы - они теряют свою талию.
Благодаря смещению можно понизить минимальное число зубьев до z=8.
Возможны два основных варианта нарезания колёс со смещением:
1.
x1=-x2
x1>0
при этом происходит утолщение зубьев шестерни и
соответствующее расширение впадин на большом колесе показать сохраняется межосевое расстояние 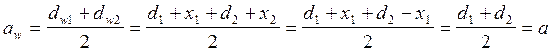
сохраняется угол зацепления
![]()
2. x1>0 и x2>0
![]()
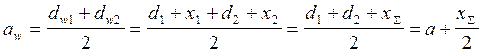
![]()
увеличения угла зацепления с 200 до 250 повышает изгибную прочность на 20 %
Кроме очевидных плюсов смещения есть и минусы: силы Fr увеличивается и соответственно возрастают потери на трение в подшипниковых опорах, возрастаю требования к жесткости валов.

Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.