Лекция 3.
Точность изготовления колёс.
Основные ошибки изготовления зубчатых колёс:
¨ ошибка шага и формы зубьев,
¨ ошибка в направлении зубьев относительно образующей делительного цилиндра.
Ошибки шага и профиля приводят к изменению мгновенного передаточного отношения i , при этом сохраняется среднее значение передаточного отношения. В измерительных, следящих механизмах это приводит к ошибке позиционирования. В высокоскоростных механизмах это приводит к повышенным динамическим нагрузкам.
Ошибки в направлении зубьев в сочетании с перекосом валов вызывают неравномерное распределение нагрузки по длине вала.
Нормы точности :
1. Норма кинематической точности. Определяется абсолютной погрешностью передаточного отношения или полной погрешностью угла поворота зубчатого колеса в пределах одного оборота.
2. Норма плавности работы. Определяется циклическими ошибками передаточного отношения или угла поворота.
3. Норма контакта зубьев. Определяется формой размерами, положением пятна контакта зубьев.
4. Боковой зазор между неработающими поверхностями зубьев. Положительное влияние при нагреве зубчатых колёс, отрицательное при реверсивной работе шестерён.
5. Шероховатость поверхностей зубьев влияет на износостойкость передач.
Степень точности по СТ СЭВ 641-77 12 степеней точности. Наиболее распространённые 6, 7 и 8 -я.
Виды сопряжения регламентируют боковой зазор
А - увеличеннй зазор,
B - нормальный зазор,
C, D - уменьшенный зазор,
E - малый зазор,
H - нулевой зазор.
7. Коэффициент расчетной нагрузки при определении контактных и изгибных напряжений зубчатых передач
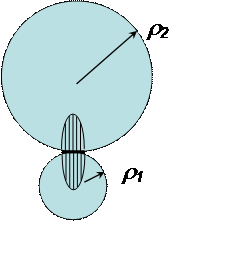
Контактные напряжения и контактная прочность при соприкосновении цилиндров произвольного радиуса
в полном виде
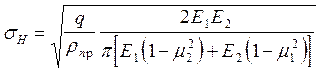
где: m - коэффициент Пуассона m=0,25¸0,35 в расчётах округлённо принимают m=0,3, с учётом этого получают (на 4)
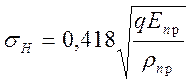 (1);
(1);
где: 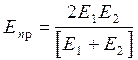
![]() для внешнего контакта (2);
для внешнего контакта (2);
(![]() - для
внутреннего)
- для
внутреннего)
хотя зубья имеют эвольвентный профиль, а не цилиндрический зона соприкосновения зубьев имеет локальный радиус кривизны, такое приближение оказывается достаточным. указанное напряжение предполагает параллельное расположение зубьев, реально в силу неточности расположения колёс зубья располагаются под углом, для учёта неравномерности распределения нагрузки в расчетах используется величина расчётная нагрузка
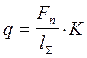 (3);
(3);
где: Fn - нормальная сила в зацеплении;
lS - суммарная длина линии контакта зубьев; нарисовать
K - коэффициент расчётной нагрузки. нарисовать варианты соприкосновения зубьев в силу того, что зубья не абсолютно жёсткие они изгибаются и начинают соприкасаться по всей длине, однако в зоне большей деформации возникает большая сила, очевидно на большей длине зуба это будет проявляться в большей степени

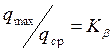 -
коэффициент концентрации нагрузки, неравномерность распределения нагрузки по длине зуба
приводит к локальному повышению как контактных напряжений
-
коэффициент концентрации нагрузки, неравномерность распределения нагрузки по длине зуба
приводит к локальному повышению как контактных напряжений![]() так и
напряжений изгиба
так и
напряжений изгиба ![]() (из прошлой лекции), соответственно существуют
(из прошлой лекции), соответственно существуют
![]() коэффициент
концентрации контактной нагрузки , и
коэффициент
концентрации контактной нагрузки , и
![]() коэффициент
концентрации изгибной нагрузки
коэффициент
концентрации изгибной нагрузки
Эти коэффициенты определяются эмпирически (на основе большого числа натурных исследований).
На этих графиках нагрузка уменьшается в соответствии с уменьшением относительной ширины колеса, которая определяется соотношением
![]() ещё раз нарисовать поверхность зуба как эвольвенту,
показать линию зацепления, основной диаметр при любых отклонениях в геометрии при изготовлении
колёс нарисовать
ещё раз нарисовать поверхность зуба как эвольвенту,
показать линию зацепления, основной диаметр при любых отклонениях в геометрии при изготовлении
колёс нарисовать
1 вариант уход точки контакта с линии зацепления;
2 вариант несоответствие шагов зацепления возникают нерасчётные напряжения, коэффициент, отражающий превышение динамических нагрузок над расчётными стационарными называется коэффициент динамической нагрузки и имеет вид
![]()
где: qv - удельная динамическая нагрузка;
q - расчётная нагрузка
9. Расчет прямозубой цилиндрической передачи на контактную прочность.
Расчёт прочности по контактным напряжениям как указывалось выше (1);
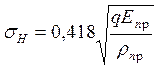 для прямозубых передач (3);
для прямозубых передач (3);
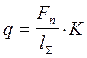
подставляя : K = KH
lS =bw ширина зуба;
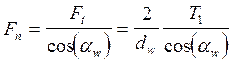 - показать на рисунке показать на рисунке что
- показать на рисунке показать на рисунке что
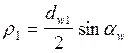 ;
; 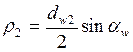
мы знаем, что 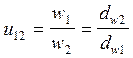 т.е.
т.е. ![]()
подставляя в (2)
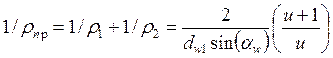 для внутреннего зацепления
для внутреннего зацепления 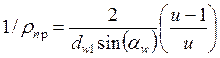
подставляя всё это в (1) получим
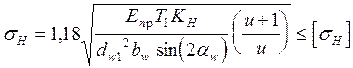
заменим 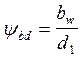
решая относительно d1 находим
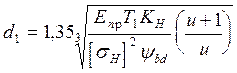
вводим коэффициент 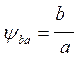
с учётом 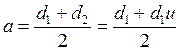 заменим
заменим
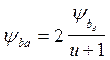
получим![]()
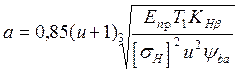
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.