
Задача №3
Определение характеристик режимов работы автохозяйства строительной организации методами марковских процессов с использованием Mathcad
Постановка задачи:
В автохозяйстве имеется n автомашин. Каждая из этих автомашин независимо от другой может выходить из строя. Интенсивность простейшего потока отказов равна λ. Отказавшая автомашина становится на стоянку и ожидает начала ремонта. Время ожидания начала ремонта распределено по показательному закону с параметром γ. Время продолжительности ремонта распределено по показательному закону с параметром μ. Определить вероятности состояний автомашины, если в начальный момент она была исправна.
Решение:
Состояния автомашины следующие:
- S0 – автомашина исправна,
- S1 – автомашина ожидает ремонта,
- S2 – автомашина ремонтируется.
Размеченный граф состояний имеет вид:
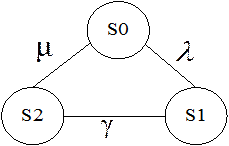
Данную задачу решим методом Рунге-Кутта с использованием ППП MATHCAD.
1. Определение исходных переменных и диапазона
γ:=3 μ:=15 λ:=3 n:=0..99
2. Массив первых производных (дифференциальный оператор) D и начальные условия задачи (для t = 0) p
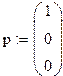
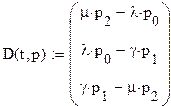
3. Решение задачи методом Рунге-Кутта
![]()
4. Графическая интерпретация решения задачи
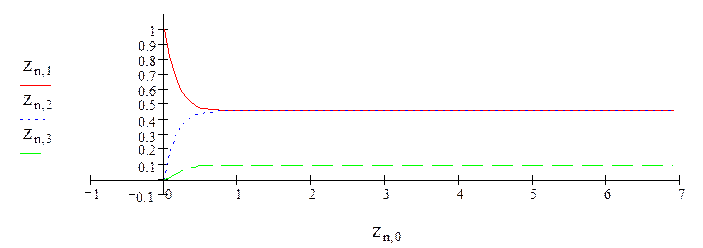
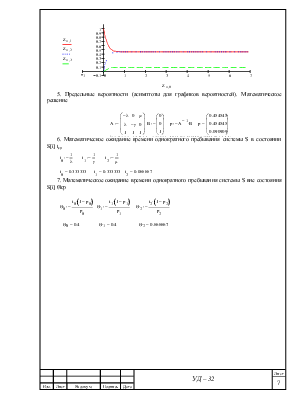
5. Предельные вероятности (асимптоты для графиков вероятностей). Математическое решение
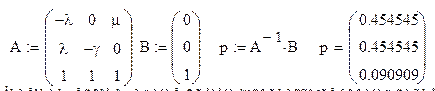
6. Математическое ожидание времени однократного пребывания системы S в состоянии S[i] tср
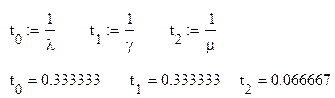
7. Математическое ожидание времени однократного пребывания системы S вне состояния S[i] Qср
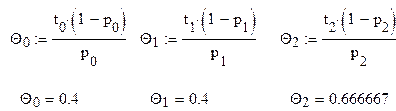
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.