Математические модели в расчетах на ЭВМ. Решение задач оптимизации средствами Mathcad и MS Excel: Лабораторный практикум

Кафедра “Информационные технологии”

Н.А. РОГАЧЁВА

МАТЕМАТИЧЕСКИЕ МОДЕЛИ

В РАСЧЕТАХ НА ЭВМ

Пособие по решению задач оптимизации

средствами MathCad и MS Excel

Одобрено методической комиссией

механического факультета БелГУТа

Гомель 2002

УДК 681.3.06  

Р 592

Р е ц е н з е н т: к.ф.-м.н., доцент кафедры “Вычислительная математика и программирование” ГГУ им. Ф. Скорины Карасева Г. Л.

Р 592 Рогачева Н.А. Математические модели в расчетах на ЭВМ. Решение задач оптимизации средствами Mathcad и MS Excel: Лабораторный практикум. – Гомель: БелГУТ, 2002. – 40с.

Изложены основные приемы решения задач оптимизации средствами MathCad и MS Excel. Рассмотрены постановка, способы решения и анализ некоторых задач линейного программирования.

Предназначено для студентов четвертого курса механического и строительного факультетов, изучающих дисциплину “Математические модели в расчетах на ЭВМ”, а также может использоваться при изучении методов оптимизации. Пособие рассчитано как на пользователей, имеющих опыт работы с электронными таблицами и средой MathCad, так и новичков.

ã Н.А. Рогачёва, 2002.

ОГЛАВЛЕНИЕ

ВВЕДЕНИЕ. 4

1 КЛАССИФИКАЦИЯ ЗАДАЧ ОПТИМИЗАЦИИ.. 4

1.1 Геометрическая интерпретация и графический метод решения задач оптимизации. 5

1.1.1 Алгоритм решения графическим методом. 5

1.1.2 Использование Mathcad для решения графическим методом. 5

1.2 Индивидуальные задания. 7

Контрольные вопросы. 9

2 ЗАДАЧА О НАЗНАЧЕНИИ.. 9

2.1 Постановка задачи. 9

2.2 Математическая модель. 10

2.3 Способы решения задачи. 10

2.3.1 Решение задачи с использованием среды МаthCаd. 10

2.3.2 Решение задачи с использованием MS Excel 11

2.4 Индивидуальные задания. 12

Контрольные вопросы. 14

3 ТРАНСПОРТНАЯ ЗАДАЧА.. 14

3.1 Постановка задачи. 14

3.2 Математическая модель задачи. 14

3.3 Способы решения задачи. 15

3.3.1 Решение транспортной задачи средствами MathCad 2000. 15

3.3.2 Решение задачи в Excel 16

3.4 Индивидуальные задания. 17

Контрольные вопросы. 17

4 ЗАДАЧА РАСПРЕДЕЛЕНИЯ РЕСУРСОВ. 18

4.1 Постановка и математическая модель. 18

4.2 Основные положения симплекс метода. 18

4.3 Анализ оптимального решения. 20

4.4 Решение ОЗЛП в MS Excel. 21

4.4.1 Отчет по результатам. 22

4.4.2 Отчет по устойчивости. 23

4.4.3 Отчет по пределам. 23

4.4.4 Параметрический анализ 24

4.5 Индивидуальные задания. 25

Контрольные вопросы. 26

СПИСОК ЛИТЕРАТУРЫ... 26

ВВЕДЕНИЕ

Важность принятия оптимальных решений, особенно в экономике при распределении ресурсов, в технике при проектировании и эксплуатации технических объектов, не вызывает сомнения. Оптимальные решения, как показывает опыт, могут быть лучше решений, принятых традиционными методами, на 5 - 15% от величины  критерия, по которому производится оптимизация. Исходя из достаточной трудоемкости применения классических методов решения задач оптимизации наиболее рациональный способ решения и проверки правильности использования традиционных методов оптимизации – это применение разработанного программного обеспечения.

В данном пособии изложены основные способы поиска оптимальных решений средствами MathCad и MSExcel. Рассмотрены постановка, решение и анализ некоторых задач линейного программирования. Пособие может помочь освоить основные приемы работы с электронными таблицами и средой MathCad. Решение всех задач описано в форме алгоритмов, представляющих собой последовательность команд среды MathCad и пакета MSExcel c пояснениями и рисунками, учитывающими специфику каждой программы. Описаны использование не только встроенных средств оптимизации, но и возможность геометрической интерпретации решения задачи линейного программирования, анализа найденного оптимального решения.

В конце каждого раздела приведены индивидуальные задания для студентов (20 вариантов) и список контрольных вопросов, при подготовке ответов на которые должны быть использованы конспект лекций по дисциплине “Математические модели в расчетах на ЭВМ”, данное издание и учебные материалы из списка литературы.

1 КЛАССИФИКАЦИЯ ЗАДАЧ ОПТИМИЗАЦИИ

Задача оптимизации в общем случае включает три составляющих: целевую функцию (критерий оптимизации), ограничения и граничные условия. Критерий оптимизации показывает влияние искомых переменных на его величину, которая должна быть максимизирована или минимизирована в зависимости от выбранного критерия. Ограничения определяют существующие связи между искомыми переменными. Граничные условия показывают предельно допустимые значения искомых переменных. Таким образом, математическая модель общей задачи оптимизации имеет вид:

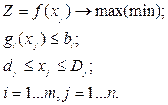
При проектировании и эксплуатации технических объектов, а также в экономике при распределении ресурсов достаточно часто имеют дело с распределительными задачами, в которых имеется ограниченное количество ресурсов, недостаточное для выполнения всех работ наилучшим образом. Необходимо распределить их так, чтобы достичь наибольшего эффекта. По наличию того или иного признака данный тип задач можно