ЗАДАЧА ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ №2
Условие задачи:
Предприятие производит два типа продукции: тип 1 и тип 2. Соответственно на изготовление двух типов продукции расходуется три вида компонентов. Доход от реализации продукции приведён в таблице:
Таблица 3.1
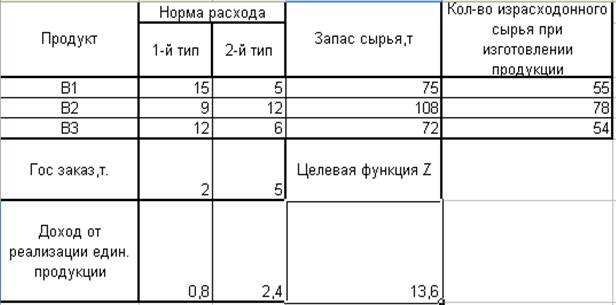
Требуется определить количество израсходованного сырья по каждому компоненту на изготовление двух типов продукции при условии максимального запаса продукции сырья на складе.
Решение:
Необходимо построить математическую модель.
Переменными в модели будут являться объём производства (в тоннах) продукции 1-го и 2-го типа - X1 и X2 соответственно. Математическая модель задачи линейного программирования включает целевую функцию и ограничения.
Целевая функция обозначается Z и находится по формуле:
Z=2* X1+6* X2 max (2)
При решении данной задачи необходимо учесть ограничения на расход исходных продуктов и на спрос.
Ограничения:
$B$11 = $B$6
$C$11 = $C$6
$E$3 <= $D$3
$E$4 <= $D$4
$E$5 <= $D$5
Таблица 3.2
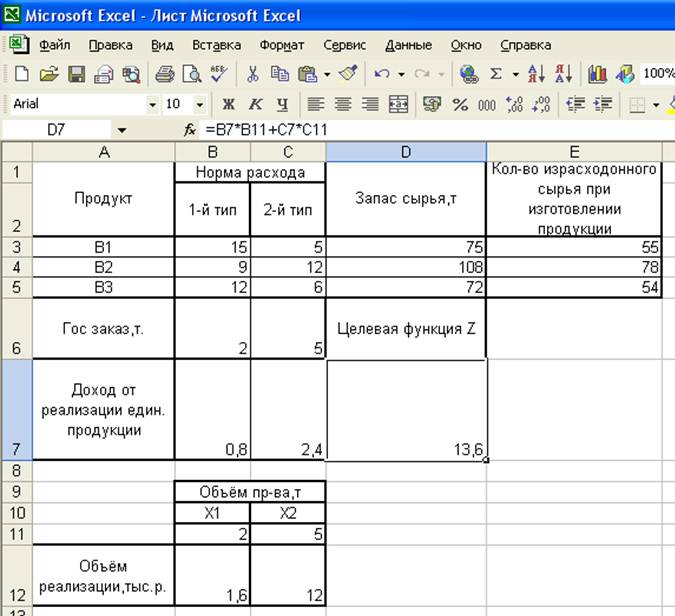
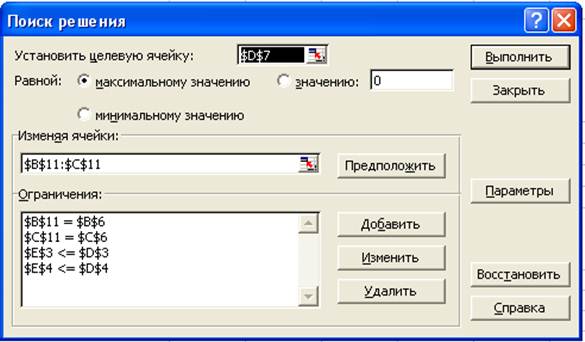
Рис. 3.1
Вывод:
Для получения максимальной прибыли от реализации продукции, при полном выполнении Госзаказа, необходимо израсходовать 55т компонента В1, 78 т компонента В2 и 54т компонента В3.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.