Разработка модели доставки груза «точно в срок» и оптимизация потерь получателя.
Доставка грузов «точно в срок» – 1 из главных целей логистики. Существует 2 взаимодополняющих решения задачи доставки грузов «точно в срок»:
– первое решение состоит в рациональном управлении материальными и информационными потоками – непрерывном отслеживании перемещения груза и в необходимых случаях приложения эффективных управляющих воздействий;
– второе решение требует согласования технических и технологических параметров субъектов логистической цепи (ЛЦ), участвующих в перевозке магистральным и промышленным транспортом, тр-ных узлов. Тр-ный узел – грузовые и сортировочные станции, тр-но-грузовые комплексы, т.е. пункты ЛЦ, на которых происходит «стыковка», обслуживание и преобразование материальных потоков.
К техническим параметрам относятся:
– перерабатывающая способность и вместимость складов, грузовых фронтов, п-о и сортировочных путей, маневровых средств (локомотивов, горок, вытяжек);
– провозная способность участков магистрального тр-та.
Технологические параметры определяются затратами времени на движение и обслуживание материального потока на перечисленных выше элементах ЛЦ, а также его мощностью. Эти параметры характеризуются временем доставки груза при обеспечении его качества и сохранности.
«Неофициальным»
параметром, оказывающим влияние на временные технологические показатели,
является фактический уровень использования технических средств (![]() ).
).![]() интерпретируется
как вероятность того, что технические средства, обслуживающие материальный
поток, являются занятыми.
интерпретируется
как вероятность того, что технические средства, обслуживающие материальный
поток, являются занятыми.
Допустимое время доставки груза получателю:
![]()
![]()
где ![]() –
допустимое отклонение времени доставки от его планового значения
–
допустимое отклонение времени доставки от его планового значения ![]() . При этом должно выполняться условие;
. При этом должно выполняться условие; ![]() – коэффициент допустимого отклонения
времени доставки по отношению к общему разрешенному времени доставки.
– коэффициент допустимого отклонения
времени доставки по отношению к общему разрешенному времени доставки.
![]()
Целевая функция
![]()
где t1,
t2 – установленное технологическое
время обслуживания материального потока i-ым
элементом ЛЦ; ![]() – вероятность отказа i-го элемена ЛЦ; Сi –
удельные потери, обусловленные отклонением фактической величины
– вероятность отказа i-го элемена ЛЦ; Сi –
удельные потери, обусловленные отклонением фактической величины ![]() от договорной
от договорной ![]() .
.
Ограничения
![]()
![]()
Данные ограничения показываются на графике
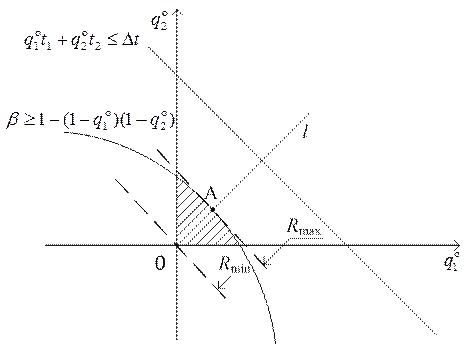
Как видно из
графика, в данном примере более сильное ограничении – ![]() (может
быть и
(может
быть и ![]() , в зависимости от исходных данных). Необходимо
решить задачу по нахождению глобального оптимума функции R
при ограничении
, в зависимости от исходных данных). Необходимо
решить задачу по нахождению глобального оптимума функции R
при ограничении ![]() . На рисунке множество допустимых
решений заштриховано. Линиями уровня функции R
являются параллельные прямые Rmax и Rmin. Очевидно, что
глобальный минимум в точке 0(0;0), а глобальный максимум – в точке А касания
прямой уровня и кривой
. На рисунке множество допустимых
решений заштриховано. Линиями уровня функции R
являются параллельные прямые Rmax и Rmin. Очевидно, что
глобальный минимум в точке 0(0;0), а глобальный максимум – в точке А касания
прямой уровня и кривой ![]() . Далее определяются
координаты точки А(
. Далее определяются
координаты точки А(![]() ). Т.о. минимальное значение
функции равно 0, когда
). Т.о. минимальное значение
функции равно 0, когда ![]() =0 и
=0 и ![]() =0, а
максимальное –
=0, а
максимальное – ![]() .
.
82 Определение экономической эффективности применения принципов в логистике при доставке грузов
Рассмотрим логистическую систему, состоящую из двух прилегающих к предприятию участков магистральной ж/д и самого предприятия, которое получает сырье и производит готовую продукцию, поставляя её на рынок сбыта. Целевая функция, выражающая экономический эффект для обоих субъектов ЛС (тр-та и поизводства):
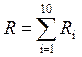
Экономия приведенных затрат на строительство складов снабжения и сбыта предприятия в результате сокращения уровня запасов
![]()
где ![]() –
сокращение уровня запасов соответственно на складах снабжения и сбыта;
–
сокращение уровня запасов соответственно на складах снабжения и сбыта; ![]() – удельная площадь, необходимая для
хранения грузовой единицы (контейнера, пакет, тонны);
– удельная площадь, необходимая для
хранения грузовой единицы (контейнера, пакет, тонны); ![]() –
стоимость строительства 1 м2 площади складов с учетом технического
–
стоимость строительства 1 м2 площади складов с учетом технического
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.