Определение времени выполнения для комплекса строительных работ

Задача №1

Требуется:

1)  Постановка задачи;

2)  Найти:   

  I.  Плановые время начала каждой работы;

  II.  Критический путь и его длину;

  III.  Полное, свободные и независимые резервы времени выполнения работ;

3)  Вывод.

Постановка задачи: для комплекса строительных работ связанных с вводом в эксплуатацию объездной дороги для крупного промышленного центра, составлен соответствующий сетевой график. В целях определения оптимальных сроков начала и завершения, как всего комплекса в целом, так и каждой работы в отдельности, оптимального графика задействования конкретных строительных бригад, необходимо рассчитать:

ü  Плановые время начала каждой работы;

ü  Критический путь и его длину;

ü  Полное, свободные и независимые резервы времени выполнения работ.

Перечень работ:

Решение:

Построим сетевой график, проложим критический путь и определим его длину (критическое время).

Критическое время – минимальное необходимое время на ввод в эксплуатацию объездной дороги.

Этого можно добиться:

1.  логическую перестановку сети так, чтобы работы, лежащие на нём, выполнялись не последовательно, а параллельно.

2.  сокращение продолжительности работ, лежащих на критическом пути.

  I  путь требует организационных мер.

  II  путь – капитальных вложений.

;

.

Определение критического пути ведётся от последнего события сети. События и работа, лежащие на критическом пути, не имеют резервов времени, и критический путь по определению выражается как самый длинный из полных путей.

Критический путь: 1-2-3-5-6

ед.вр.

Резерв времени для событий, лежащих на критическом  пути, , т.к.   показывает, на какое время может задержать событие, не изменяя общего срока выполнения процесса. Для работ, не лежащих на критическом пути, резервы времени выполнения работ вычисляются по следующим формулам:

;       ; .

Расчёты приведём в табличную форму:

Вывод: таким образом, работы имеют резервы, следовательно, необходимые ресурсы на их выполнение можно использовать на других строительных участках.

Задача №2

Требуется:

1)  Постановка задачи;

2)  Построение линейного графика комплекса работ;    

3)  Нахождение критического срока, критических и некритических работ, полные и свободные резервы  некритических работ.

4)  Вывод.

Постановка задачи: для перевода производства на более интенсивную технологию необходимо осуществить комплекс подготовительных работ. С этой целью создана группа специалистов и составлен сетевой график выполнения работ.

Решение: известна продолжительность, , выполнения каждой работы. По данному графику построить линейный график (линейную диаграмму) комплекса работ и найти по нему критический срок, критических и некритических работ, полные и свободные резервы некритических работ.

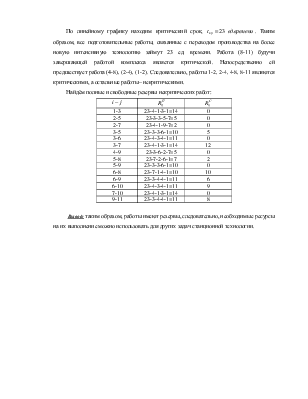
По линейному графику находим критический срок, . Таким образом, все подготовительные работы, связанные с переводом производства на более новую интенсивную технологию займут 23 ед. времени. Работа (8-11) будучи завершающей работой комплекса является критической. Непосредственно ей предшествует работа (4-8), (2-4), (1-2). Следовательно, работы 1-2, 2-4, 4-8, 8-11 являются критическими, а остальные работы– некритическими.

Найдём полные и свободные резервы некритических работ:

Вывод: таким образом, работы имеют резервы, следовательно, необходимые ресурсы на их выполнение можно использовать для других задач станционной технологии.