Другие предметы \ Детали машин

Расчёт цилиндрической зубчатой передачи. Коэффициент долговечности. Материалы зубчатых колёс и допускаемые напряжения. Проектные и проверочные расчёты, страница 5

Опыт проектирования показывает, что для прирабатывающихся колёс изгибная прочность не является главным критерием и применение мелкомодульных колёс вполне обосновано.При больших числах зубьев (и малых модулях) повышаются коэффициент перекрытия, плавность работы передачи и нагрузочная способность. Иногда окончательное решение по назначению модуля принимают после расчёта z_Sи z₁. Суммарное число зубьев

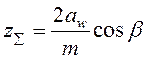, (28)

где b— угол наклона линии зуба, в прямозубых колёсах b= 0, в косозубых рекомендуется b = 8...15° (20°), в шевронных и с раздвоенной ступенью b = 25...40°.

Выбором стандартных a_w добиваются целых значений z_S прямозубого зацепления. В косозубых передачах z_S округляют до ближайшего целого и уточняют угол наклона:

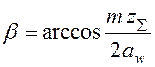, (29)

который должен быть больше минимального b_min, обеспечивающего осевой коэффициент перекрытия e_b ³ 1,12;

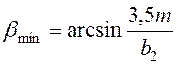, (30)

где b₂ – ширина венца колеса, которую определяют по формуле

. (31)

Ширина венца шестерни

b₁= 1,12·b₁. (32)

Ширину венцов округляют по ГОСТ 6636 (Прил. В). Число зубьев шестерни:

. (33)

Его рекомендуется принимать в пределах z₁ = 20...30, вписывание в которые, возможно, потребует изменения модуля и пересчета z_S и z₁ по формулам (28) и (33). Следует помнить, что минимально допустимое число зубьев шестерни из условия неподрезания

. (34)

При z₁< z_min принимают равносмещенное зацепление с коэффициентом смещения шестерни

(35)

и коэффициентом смещения колеса x₂ = - x₁. Геометрические параметры определяют по следующим формулам (для косозубого зацепления без смешения), в мм:

делительные диаметры:

; (36)

диаметры вершин и впадин:

; (37)

. (38)

Окружная скорость колёс (м/с):

u = π·d·n/60000. (39)

После определения геометрических параметров и окружной скорости уточняют коэффициенты К_Н_aи K_Н_uи выполняют проверочный расчёт по контактным напряжениям. Рабочее контактное напряжение в МПа

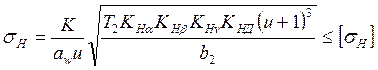. (40)

Вращающий момент на валу колеса Т₂ следует ставить в формулу (40) в Н×мм. По контактным напряжениям допускается перегрузка до 3% и недогрузка до 10%. Приводить в соответствие рабочие и допускаемые контактные напряжения рекомендуется изменением ширины венца колеса. Для расчёта изгибных напряжений и валов определяют усилия в зацеплении. Окружное усилие в Н:

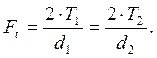(41)

Радиальное усилие:

F_r= F_t_·tga/cosb. (42)

Осевое усилие:

F_a= F_t_·tgb. (43)

В шевронных передачах F_a=0; в передачах с раздвоенной ступенью в каждом зацеплении силы F_t , F_rи F_a,определённые по формулам (41) … (43), делят пополам.