А – площадь поперечного сечения ремня, м2.
Влияние центробежных сил сказывается при
больших скоростях (u > 20 м/с). Сила ![]() , действующая на валы передачи,
определяется как геометрическая сумма усилий F1 и F2 либо, упрощенно, двух сил Fo (рис. 17.6, а). В практических расчётах принимают Fo» 1,5 Ft. Сила, действующая на валы:
, действующая на валы передачи,
определяется как геометрическая сумма усилий F1 и F2 либо, упрощенно, двух сил Fo (рис. 17.6, а). В практических расчётах принимают Fo» 1,5 Ft. Сила, действующая на валы:
![]() (17.18)
(17.18)
17.7. Напряжения в ремне
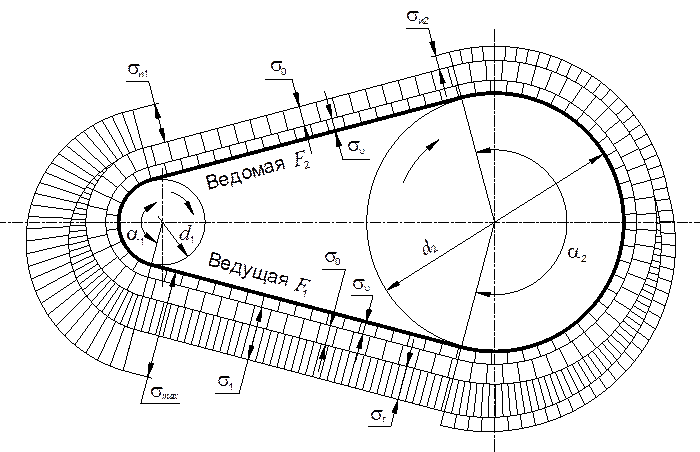 Наибольшие
напряжения создаются в ведущей ветви ремня (рис. 17.7), в точке её набегания на
малый шкив, где складываются напряжения в ведущей ветви s1,
напряжения от центробежных сил su и напряжения изгиба sи при
огибании ремнем шкива.
Наибольшие
напряжения создаются в ведущей ветви ремня (рис. 17.7), в точке её набегания на
малый шкив, где складываются напряжения в ведущей ветви s1,
напряжения от центробежных сил su и напряжения изгиба sи при
огибании ремнем шкива.
Рис. 17.7. Напряжения в работающем ремне
А) Напряжения в ведущей ветви с учётом формулы (17.10):
![]() (17.19)
(17.19)
Анализ формулы (17.16) показывает, что напряжение st возрастает с увеличением so. Однако практика показывает значительное снижение долговечности ремня с увеличением so. Поэтому рекомендуют принимать напряжения, выработанные практикой проектирования:
so £ 1,5 МПа – для клиновых ремней;
so £ 1,8 МПа – для плоских ремней.
Значение полезного напряжения st влияет на долговечность примерно так же, как и so. При указанных значениях so допустимое значение st не превышает 2…2,5 МПа.
Б) Напряжение от центробежной силы:
![]() (17.20)
(17.20)
Если для оценивания значений напряжений от центробежных сил приблизительно принять r = 1000 кг/м3, то:
при u = 10 м/с su = 0,1 МПа;
при u = 20 м/с su = 0,4 МПа;
при u = 40 м/с su = 1,6 МПа.
Таким образом, для наиболее распространенных на практике тихоходных (u < 10 м/с) и среднескоростных (u < 20 м/с) ремённых передач влияние su несущественно.
В) Напряжение изгиба при огибании ремнем шкивов определяют по закону Гука:
![]() (17.21)
(17.21)
где e – относительное удлинение наружных волокон.
При чистом изгибе:
![]() ,
,
где y – расстояние от нейтрального слоя;
r – радиус кривизны нейтрального слоя.
Для ремня: y = d/2; r = d/2, откуда:
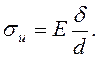 (17.22)
(17.22)
Приняв Е = 100 МПа (Е = 80…100 МПа для резинотканевых ремней), оценивают значения напряжений от изгиба ремня:
при d/d = 100 sи = 1 МПа;
при d/d = 50 sи = 2 МПа;
при d/d = 25 sи = 4 МПа.
Реальные отношения d/d ближе к нижней цифре, следовательно, напряжения изгиба являются наиболее опасными для работоспособности ремня. Приведенные цифры это подтверждают. Суммарное максимальное напряжение в ведущей ветви в месте набегания ремня на малый шкив:
![]() (17.23)
(17.23)
17.8. Долговечность ремня
Опыт эксплуатации ремённых передач показал, что их работоспособность ограничена тяговой способностью и долговечностью ремня. В первом случае ремень теряет тяговую способность из-за буксования в связи с недостаточной прочностью сцепления ремня со шкивом. Во втором случае выход из строя передачи связан с усталостным разрушением ремня.
Тяговая способность – сложный критерий, учитывающий прочность материала ремня и его способность к сцеплению с материалом шкива. Параметры этого критерия рассчитывают на основании экспериментальных данных (см. п. 17.9). Долговечность (ресурс) определяют по формуле:
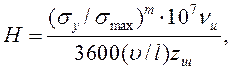 (17.24)
(17.24)
где sy – предел выносливости; для клиновых ремней sy = 9 МПа при m = 11;
m – показатель степени кривой выносливости;
107 – базовое число циклов;
![]() – коэффициент,
зависящий от отношения sр/sи; при sр/sи = 0,5
– коэффициент,
зависящий от отношения sр/sи; при sр/sи = 0,5 ![]() = 2;
= 2;
u – скорость ремня в м/с;
l – длина ремня в м;
zш – число шкивов; на рис. 17.1 и 17,6 zш = 2:
![]() (17.25)
(17.25)
sр – напряжение растяжения, которое складывается из напряжения в ведущей ветви и напряжения от центробежных сил;
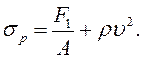 (17.26)
(17.26)
Напряжение изгиба определяется по формуле (17.22). Нормативный ресурс зависит от режима нагрузки и составляет Н0 = 1000…5000 ч.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.