Ремённые передачи. Материалы ремней. Способы натяжения ремней. Кинематика и геометрия. Силы в передаче, страница 2

          4. Низкая долговечность ремня (Н = 1000…5000 ч).

          Ремённую передачу применяют как понижающую передачу, а также для смягчения колебаний нагрузки и для перекрытия больших межосевых расстояний. Мощность обычно не превышает 50 кВт. В комбинации с другими передачами ремённую передачу используют в быстроходной ступени, устанавливая ведущий шкив на вал двигателя. Применяют ремённые передачи в металлорежущих станках, автомобилях, сельскохозяйственных машинах, в приводах грузоподъёмных, строительных, путевых и других машин.

17.5. Кинематика и геометрия

          Вследствие упругого скольжения скорость ведомого шкива меньше скорости ведущего:

 или                        (17.1)

   где  s – коэффициент скольжения; s = 0,01…0,02;

         и- диаметры малого и большого шкивов.

          При этом передаточное отношение:

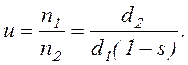                                               (17.2)

          В открытой ремённой передачи (рис. 17.5) показаны: а – межосевое расстояние; a – угол обхвата малого шкива; l – длина ремня. Вследствие вытяжки и провисания ремня значения a и l не являются точными и определяются приближённо. Угол обхвата:

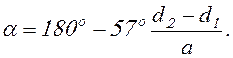                                        (17.3)

          Длину ремня определяют как сумму прямолинейных участков и дуг обхвата:

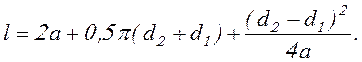                            (17.4)

          Для бесконечных ремней после принятия стандартной длины уточняют межосевое расстояние:

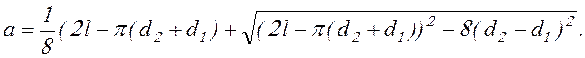           (17.5)

 

Рис. 17.5. Геометрические параметры передачи

17.6. Силы в передаче

          Нагружение ремня рассмотрено для двух случаев: крутящий момент Т₁ = 0 (рис. 17.6, а) и Т₁ > 0 (рис. 17.6, б). Обозначено: F₀ – предварительное натяжение ремня; F₁ и F₂ – натяжения ведущей и ведомой ветвей в нагруженной передаче. Из уравнения моментов находят:

 

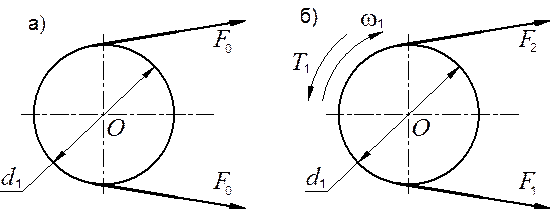Рис. 17.6. Усилия в ветвях

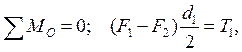                             откуда

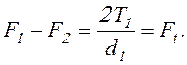                                                (17.6)

          При установлении связи между усилиями исходят из предположения, что длина ремня остается неизменной как в ненагруженной, так и в нагруженной передаче. Следовательно, дополнительная вытяжка ведущей ветви компенсируется равным сокращением ведомой ветви. Равные деформации вызываются равными силами DF:

;                                              (17.7)

.                                             (17.8)

          Из равенств (17.7) и (17.8) следует:

                                             (17.9)

          А из равенств (17.6) и (17.9) находят искомые соотношения:

;                                          (17.10)

.                                          (17.11)

          Таким образом, в нагруженной передаче усилие в ведущей ветви увеличивается на половину полезной нагрузки . Уравнения (17.10) и (17.11) не вскрывают тяговой способности передачи, которая связана с величиной трения между ремнем и шкивом. Такая связь установлена Эйлером в виде:

                                         (17.12)

   где е – основание натурального логарифма;

f – коэффициент трения.

          Решая совместно уравнения (17.6), (17.9) и (17.12), находят:

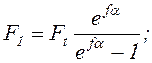                                            (17.13)

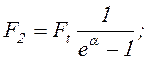                                            (17.14)

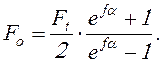                                          (17.15)

          Поделив левую и правую части уравнения (17.15) на площадь сечения ремня А, получают зависимости между напряжениями:

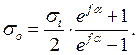                                              (17.16)

Полученные формулы устанавливают связь сил натяжения ветвей и напряжений в них с полезной нагрузкой и факторами трения f и a. Анализ формулы (17.15) методом конечных элементов показывает, что:

          – при     fa®¥:   ; это идеальная передача;

          – при     fa® 0:    ; такая передача неработоспособна.

          Следовательно, увеличение f  и a благоприятно сказывается на работе передачи. Эти выводы приняты за основу при создании конструкций клиноремённой передачи, где приведенный коэффициент трения f¢ = f /sin(φ/2),  и передачи с натяжным роликом (a > 180°).

          Центробежная сила F_u ослабляет полезное действие предварительного натяжения F_o, уменьшая силу трения и дополнительно нагружая ветви ремней:

                                                  (17.17)

   где  r – плотность материала ремня; r  = 1100…1200 кг/м³ для резинотканевых ремней;