Упругие муфты. Управляемые муфты. Автоматические муфты. Фрикционные передачи, страница 5

На величину площадки скольжения влияют материалы катков и величина нагрузки . С увеличением нагрузки точка в приближается к точке а, дуга скольжения распространяется на всю дугу контакта и упругое скольжение переходит в буксование. Формула (28.7) свидетельствует о непостоянстве передаточного отношения, так как содержит переменную величину s.

Геометрическое скольжение связано с неравенством скоростей на площадке контакта у ведущего и ведомого катков. Оно является решающим для фрикционных передач. Поиски новых форм тел качения часто связаны со стремлением уменьшить геометрическое скольжение.

В лобовом вариаторе (рис. 28.4) окружная скорость на рабочей поверхности ролика постоянна по всей ширине его и равна . Скорость различных точек диска  изменяется пропорционально расстоянию этих точек от центра (на краю диска ). Скорости  и  на линии контакта должны быть равны между собой. Однако в данной конструкции равенство скоростей можно получить только для какой-то одной точки линии контакта. Эту точку Pназывают полюсом качения. Через полюс качения проходит расчётная окружность диаметром . Во всех других точках линии контакта наблюдается скольжение со скоростью .

Полюс качения располагается в середине линии контакта только при холостом ходе. При работе под нагрузкой он смещается от середины к периферии диска. Это объясняется уменьшением скорости ведомого звена вследствие упругого скольжения.

 

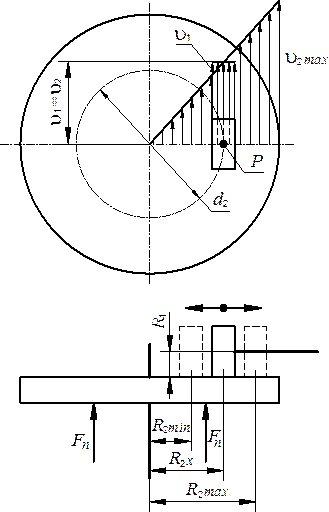Рис. 28.4. Геометрическое скольжение

28.4. Виды разрушения и критерии расчёта

При работе фрикционных пар происходят следующие виды разрушения рабочих поверхностей:

1) усталостное выкрашивание – в передачах, состоящих из стальных катков, работающих в масле при полужидкостном трении; это связано с действием переменных контактных напряжений (рис. 2.11 в лекции №2);

2) износ – в передачах, работающих без смазки;

3) задир поверхности связан с буксованием или перегревом передачи при больших скоростях и нагрузках в условиях недостаточной смазки.

Все перечисленные виды разрушения зависят от напряжений в месте контакта. Поэтому основным критерием работоспособности и расчёта является контактная прочность. При использовании неметаллических материалов ведется расчёт по удельной нагрузке.

28.5. Расчёт по контактным напряжениям

В цилиндрической фрикционной передаче расчёт ведут по контактным напряжениям при начальном контакте по линии в соответствии с формулой Герца:

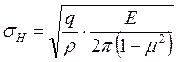,                                                (28.8)

где q – удельная нагрузка;

,                                                       (28.9)

b– длина контактной площадки (ширина катка, рис. 28.1);

E – приведенный модуль упругости.

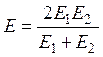;                                                   (28.10)

 – приведенный радиус кривизны:

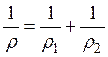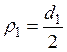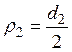          ;           ;        ;                          (28.11)

μ – коэффициент Пуассона.

Принимая μ = 0,3, получают формулу Герца, пригодную для расчёта передач со стальными и чугунными катками:

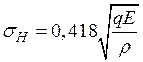.                                            (28.12)

Подставляя в формулу Герца параметры фрикционной передачи

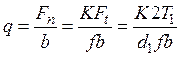,                                 (28.13)

и пренебрегая скольжением, выводят зависимость диаметра малого катка  от межосевого расстояния:

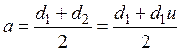,        откуда 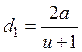.                      (28.14)

Удельная нагрузка

;

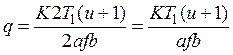кривизна

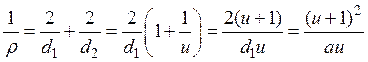.                          (28.15)

Контактные напряжения

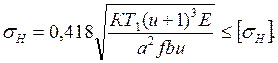                                (28.16)

Формула (11.21) пригодна только для проверочного расчета. Для вывода формулы проектного расчета вводят коэффициент ширины

;  .                                (28.17)

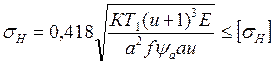,            откуда

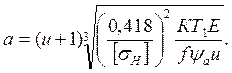                                   (28.18)

Для металлической пары при работе в масле =(2,5…3) HB МПа; для катков из текстолита  = 80…100 МПа.

28.6. Расчёт по удельной нагрузке

Для фрикционных передач с низкой прочностью материалов ограничивают нагрузку, приходящуюся на единицу длины, по условию:

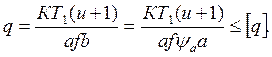                                 (28.19)

Отсюда межосевое расстояние

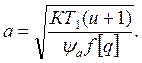                                             (28.20)

= 30…60 Н/мм – для чугуна по прессованной бумаге;

= 2,5…5 Н/мм – для чугуна по резине.