Виды нагрузок и вызываемые ими напряжения. Допускаемые напряжения. Факторы, влияющие на прочность, страница 3

2.6.4. Число циклов нагружения

Найденный из кривой выносливости (рис. 2.6) предел выносливости , внесенный в справочники, соответствует базовому числу циклов N_G. База напряжений, то есть точка перехода кривой выносливости в прямую, зависит от вида деформации и свойств материала. Например, база изгибных напряжений зубьев колес N_FG = 4·10⁶. Для вращательного движения число циклов нагружения (наработку) определяют по формуле:

N = 60·n·L_h,                                                           (2.10)

где  n – частота вращения в об/мин; L_h – долговечность, ч.

Если наработка N меньше базы N_G, то в соответствии с кривой выносливости (рис. 2.6) предельное напряжение должно быть выше. Уравнение кривой выносливости:

.                                               (2.11)

Из него находят предел выносливости  при числе циклов N:

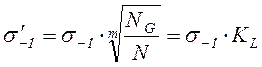,                                  (2.12)

где  m – показатель степени кривой выносливости, характеризующий крутизну ветви кривой выносливости, который колеблется в весьма широких пределах в зависимости от размеров образца, наличия концентрации напряжений, упрочнения материала и др.; так, для стальных зубчатых колёс m = 3при расчёте на контактную прочность, m = 6 или 9 – при расчёте на изгиб в зависимости от термообработки.

K_L – коэффициент долговечности; , так как предел выносливости  в забазовой области не может быть меньше предела выносливости , принятого из справочника. При расчёте зубчатых колес вводят коэффициент долговечности, определяемый как обратная величина K_L.

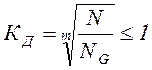.                                           (2.13)

NB 2.6. При наработке меньше базовой предельные напряжения металла увеличиваются в соответствии с кривой выносливости.

Пример 2.1. Рассчитать коэффициент долговечности зубчатых передач из объёмно закалённых колёс по контактным напряжениям, если ресурс передачи L_h= 8000 ч, частота вращения колеса n = 40 об/мин, база контактных напряжений N_G = 36·10⁶.

Решение.

Число циклов нагружения по формуле (2.10):   N = 60·40·8000 =19,2·10⁶.

Коэффициент долговечности – формула (2.13):

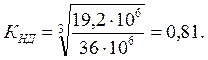
Рассмотренные факторы учитываются при циклической нагрузке, в расчётах деталей на выносливость.

2.7. Коэффициенты запаса прочности

В инженерных расчётах наибольшее распространение получил расчёт по запасам прочности. Условие прочностной надежности при такой оценке имеет вид:

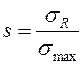.                                                      (2.14)

В частности, для пластичного материала коэффициент запаса по текучести определяют по формуле:

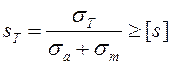.                                                 (2.15)

От правильности назначения s_T зависит степень рациональности конструкции детали. При этом заниженное значение запаса прочности может привести к разрушению детали, завышенное – к неоправданному увеличению массы изделия и перерасходу материала. Факторы, влияющие на запас прочности, многочисленны и разнообразны. Их полный учёт невозможен в связи с взаимоисключением некоторых из них. Принята методика определения допускаемого коэффициента запаса дифференцированным методом. Он заключается в определении  как произведения минимального числа коэффициентов

= s₁· s₂· s₃,                                               (2.16)

где  s₁ – коэффициент, учитывающий точность расчётной схемы, s₁=1…1,5;

s₂ – коэффициент, учитывающий однородность механических свойств материала, s₂=1,2…1,5;

s₃ – коэффициент, учитывающий специфические требования безопасности, s₃=1…1,5.

Обычно [s] =1,5….2. В каждой отрасли машиностроения выработаны свои нормы запасов прочности для конкретных деталей. Так, например, для стальных зубчатых колёс, подвергнутых объёмной закалке, рекомендуется коэффициент запаса по изгибным напряжениям = 1,8 [9].

При циклической нагрузке на прочность оказывают влияние концентрация напряжений и другие факторы, учитываемые соответствующими коэффициентами. Коэффициенты запаса соответственно по нормальным и касательным напряжениям:

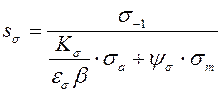;                                        (2.17)

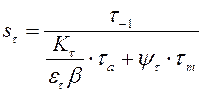.                                            (2.18)

В формулах (2.17) и (2.18)  и  - коэффициенты, учитывающие чувствительность материала к асимметрии цикла; = 0…0,15; = 0…0,1 [9]. Общий коэффициент запаса:

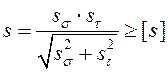.                                        (2.19)

Обычно [s] > 1,5. При расчёте валов рекомендуется  [s] = 2,5…3,5, что гарантирует не только прочность, но и достаточную жёсткость.