Самоторможение и КПД. Напряжения в резьбе. Виды разрушения резьбовых деталей. Классификация болтовых соединений

Лекция №6

5.7.2. Самоторможение и КПД

Условие самоторможения в резьбе можно записать в виде Т_РО > 0. Из формулы (5.11) следует:

 или  ψ < φʹ.                                              (5.13)

Условие ψ < φʹ называют условием самоторможения резьбы. В метрической резьбе с крупным шагом это условие выполняется, так как угол подъёма ψ = 2,5…3,5º, а приведенный угол трения φʹ = 6…16º при fʹ = 0,1…0,3. Поэтому все крепёжные резьбы самотормозящие. Это, однако, не значит, что резьбовые соединения не нуждаются в стопорении (см. п. 5.6).

NB 5.6. В самотормозящей резьбе угол подъёма резьбы больше угла трения.

КПД винтовой пары вычисляют по отношению работы, затраченной на завинчивание гайки без учета трения, к той же работе с учетом трения:

А = Т_РЗ j .                                                    (5.14)

Так как углы поворота гаечного ключа j  в обоих случаях одинаковы, то отношение работ равно отношению моментов, то есть

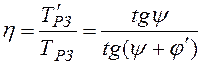 .                                            (5.15)

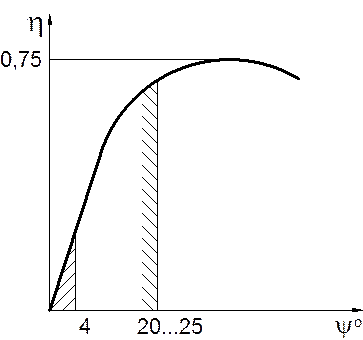Анализ формулы (5.15) показывает, что при увеличении угла подъёма  числитель и знаменатель сближаются и КПД винтовой пары повышается, что представлено на графике (рис. 5.15).

Рис. 5.15. График зависимости КПД от угла подъёма

Для увеличения  в винтовых механизмах применяют многозаходные резьбы. В практике используют винты, у которых больше  25^о, так как дальнейший прирост КПД незначителен, а изготовление резьбы затруднительно по технологическим причинам. При таких  и  = 6^омаксимально возможный КПД h = 0,75. На графике (рис. 5.15) выделены зоны крепёжных резьб (4 ^о) и ходовых резьб ( 25 ^о). Моменты завинчивания и другие параметры некоторых резьб приведены в прил. 12.

5.7.3. Распределение нагрузки по виткам

В резьбовом соединении (рис. 5.16) осевая нагрузка винта F_а передается через резьбу гайке и уравновешивается реакцией её опоры. Каждый виток резьбы нагружается соответственно силами F₁, F₂ и т.д. до F_z, где z – число витков резьбы гайки. Сумма 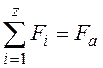. По причине различных деформаций витков F_i не равны друг другу. Задача о распределении нагрузки по виткам статически неопределима. Для её решения уравнения равновесия дополняют уравнениями деформаций. Впервые она была решена для десятивитковой гайки  Н.Е. Жуковским в 1902 г. (на рис. 5.16 показаны 6 витков из десяти).

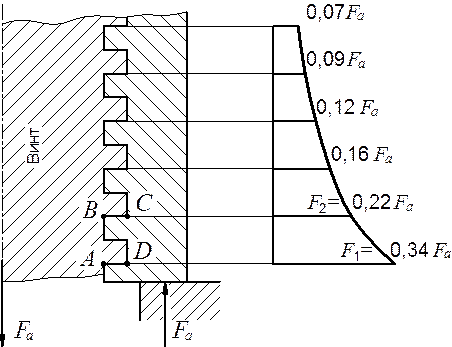Рис. 5.16. Распределение нагрузки по виткам гайки

Вследствие различного знака деформаций винта и гайки (винт растягивается, а гайка сжимается) нагрузка по виткам распределяется неравномерно. Обозначим Δ_А, Δ_В, Δ_С, Δ_D – перемещения соответствующих точек. Вследствие растяжения участка АВ винта:

                                                     (5.16)

а вследствие сжатия участка CD гайки:

                                                       (5.17)

Относительное перемещение точек А и D, В и С:

                      (5.18)

С учетом (5.16) и (5.17) находим:

                                                   (5.19)

Следовательно, деформация и нагрузка первого витка больше нагрузки второго и т.д. График распределения нагрузки по виткам гайки свидетельствует о значительной перегрузке нижних витков и о нецелесообразном увеличении числа витков стандартной гайки с Н = 0,8d, так как последние витки мало нагружены. По этому условию нецелесообразно применение мелких резьб.

Выравнивание нагрузки в резьбе можно обеспечить следующими мерами:

1) повышением податливости резьбовых деталей в зоне концентрации нагрузки (по нижним виткам);

2) созданием деформаций одного знака.

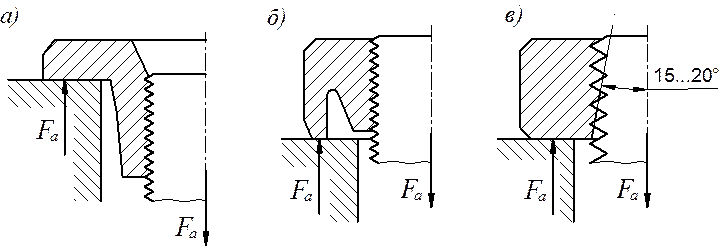          Обе меры реализованы в конструкции «висячей гайки» (рис. 5.17, а). Разновидность висячей гайки – гайка с кольцевой выточкой (рис. 5.17, б).

Рис. 5.17. Конструкции соединений для выравнивания нагрузки между витками

В этих конструкциях более высокая податливость гайки обеспечивается уменьшением её сечения в зоне концентрации нагрузки путем формирования конических поверхностей. В конструкции на рис. 5.17, в за счет среза вершин нижних витков резьбы гайки и уменьшения опорной поверхности витков винта повышается податливость последних. Применение специальных гаек позволяет повысить усталостную выносливость на 20…30%.

5.8. Напряжения в резьбе

Резьба находится в сложном напряжённом состоянии (рис. 5.18). При действии осевой нагрузки F_а  по цилиндру диаметром d₁ возникают напряжения среза t. В тех же сечениях возникают напряжения изгиба s_и. Напряжения смятия s_см расположены нормально рабочим поверхностям. Нормальные напряжения растяжения от силы F_а  приложены к опасному сечению диаметра d₁.

Параметры стандартной резьбы и резьбовых деталей принимаются из условия равнопрочности резьбы и стержня винта. В соответствии с этим условием высоту нормальных стандартных гаек принимают (рис. 5.19, а):

                                                     (5.20)

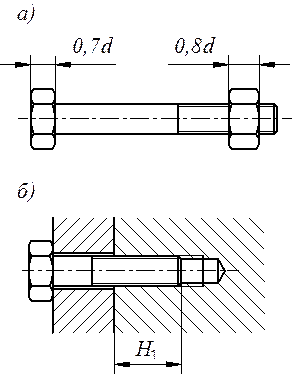          По тем же соображениям устанавливают глубину завинчивания винтов и шпилек в детали: в стальные детали Н₁ = d, в чугунные и силуминовые Н₁ = 1,5d (рис. 5.19, б).

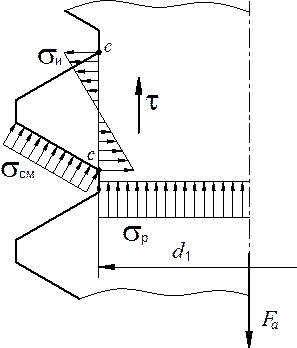
            Рис. 5.18. Напряжения в резьбе              Рис. 5.19. Резьбовые детали

NB 5.7. Параметры стандартных резьб исключают необходимость их расчёта на прочность.

5.9. Виды разрушения резьбовых деталей

Опыт эксплуатации машин показывает, что  характерными видами отказов болтовых соединений являются разрушения деталей или их элементов и нарушение стабильности затяжки. Разрушение деталей происходит, как правило, из-за среза витков резьбы, а также из-за разрушения болтов и шпилек по резьбовой части. При статических перегрузках происходит обрыв стержня, срез , изгиб и смятие резьбы на болте и  гайке.