Планирование маршрутов перевозки грузов на автомобильном транспорте

Министерство образования и науки Российской Федерации

Федеральное агентство по образованию

Государственное образовательное учреждение

 высшего профессионального образования

«Комсомольский-на-Амуре государственный

технический университет»

Факультет экономики и менеджмента

Кафедра маркетинга и коммерции

РАСЧЁТНО-ГРАФИЧЕСКОЕ ЗАДАНИЕ

по дисциплине «Транспортное обеспечение коммерческой деятельности»

Планирование маршрутов перевозки грузов

на автомобильном транспорте

1 вариант

Студент группы 5КО-1                                                                    Е.М. Понкратова

Преподаватель                                                                                 И.В. Макурин

2009

Целью выполнения расчётно-графического задания является закрепление навыков разработки маршрутов автомобильных перевозок и организации их оперативного планирования.

Исходные данные матрицы расстояний представлены в таблице 1.

Таблица 1 - Матрица расстояний

		Наименование конечного пункта
		1	2	3	4
Наименование начального пункта	1	∞	2	2,5	3
	2	2	∞	2,5	2
	3	3	2	∞	3
	4	4	1,5	2,5	∞

Произведём приведение исходной матрицы расстояний С по строкам и столбцам. Для этого из каждого элемента полученной матрицы вычтем наименьший элемент соответствующей строки. Затем из полученных элементов каждого столбца новой матрицы вычтем наименьший элемент этого столбца. Результаты приведения исходной матрицы расстояний показаны в таблице 2.

Таблица 2 - Приведённая матрица расстояний

		Наименование конечного пункта				Минимальный элемент в строке
		1	2	3	4
Наименование начального пункта	1	∞	00	00	1	2
	2	01	∞	00	01	2
	3	1	01	∞	1	2
	4	2,5	00,5	0,5	∞	1,5
Минимальный элемент в столбце		0	0	0,5	0	8

Как видно из таблицы 2, сумма минимальных элементов или констант приведения равна 8. В дальнейшем она будет задавать уровень оценки исходного множества циклов перевозки G₀. Это означает, что оценка нижней границы протяжённости для всех маршрутов устанавливается на уровне 8 км.

Далее определяем участки, подлежащие первоочередному включению в составляемый маршрут. При этом учитываем, что наличие нулевых элементов в полученной матрице указывает на минимальные по протяжённости маршруты. В связи с этим при определении порядка объезда в первую очередь должны учитываться такие элементы. Для обеспечения возможности выбора в пользу конкретного участка определяем оценки всех нулевых элементов приведённой матрицы. Полученные таким образом оценки проставляем в правом верхнем углу клетки с нулевым элементом.

Исходное множество циклов перевозки G₀ делится на два непересекающихся подмножества  и .

Подмножество  получается из множества G₀  при условии действия предположения о том, что автомобиль следует непосредственно из пункта 2 в пункт 1. В этом случае строим матрицу , соответствующая подмножеству  .

Построение матрицы  начинаем с вычёркивания второй строки и первого столбца, поскольку автомобиль может въезжать и выезжать из каждого пункта только один раз. Затем запрещается переезд из пункта 1 в пункт 2 ( → ∞). Построение матрицы  завершается с окончанием процесса её приведения.

Матрица с исключёнными второй строкой и первым столбцом представлена в таблице 3.

Оценка подмножества  равна сумме оценок исходного множества G₀  и константа приведения:

ξ() = 8 + 1 = 9.

Таблица 3 - Матрица с исключёнными второй строкой и первым столбцом

		Наименование конечного пункта			Минимальный элемент в строке
		2	3	4
Наименование начального пункта	1	∞	00,5	00	0
	3	00	∞	00	0
	4	00,5	0,5	∞	0
Минимальный элемент в столбце		0	0	1	1

В свою очередь, подмножество  образуется из множества исходя из того, что автомобилю запрещён непосредственный переход из пункта 2 в пункт 1. При этом оценка подмножества  равна сумме оценок исходного множества G₀ и нулевого элемента матрицы С₂₁:

ξ() = 8 + 1 = 9.

Далее определяем претендентов на ветвление. Для этого определяем оценки для всех нулевых элементов матрицы . Сравнение полученных оценок показало, что имеются два претендента:

1) участок (1, 3);

2) участок (4, 2).

С учётом того, что в маршрут был включён участок, заканчивающийся в пункте 1, целесообразным считается использование участка (1, 3).

После этого произведём деление подмножества  на  и  . Подмножество  получается из множества   при условии, что автомобиль следует непосредственно из пункта 1 в пункт 3. В этом случае строим матрицу . Результаты построения матрицы  представлены в форме таблицы 4.

Таблица 4 - Матрица с исключёнными первой строкой и третьим столбцом

		Наименование конечного пункта		Минимальный элемент в строке
		2	4
Наименование начального пункта	3	00	0∞	0
	4	0∞	∞	0
Минимальный элемент в столбце		0	0	0

Оценка подмножества  равна сумме оценок исходного множества  и констант произведения:

ξ() = 9 + 0 = 9.

Подмножество  образуется из множества  исходя из того, что автомобилю запрещён непосредственный переход из пункта 1 в пункт 3. При этом оценка подмножества  равна сумме оценок исходного множества  и нулевого элемента матрицы С₁₃:

ξ() = 9 + 0,5 = 9,5.

Поскольку ξ() < ξ(), то в дальнейшем ветвлению подлежит подмножество . Однако матрица  имеет размерность 2×2, в связи, с чем ветвление подмножества  не представляется возможным. Учитывая это обстоятельство, составляем окончательный вариант маршрута.

Затем определяем оценки нулевых элементов матрицы . Как видно из таблицы 4, оценку «∞» имеют два элемента С₃₄ и С₄₂. Следовательно, правом на приоритетное включение в состав маршрута обладают два участка:

- участок, предусматривающий переход из пункта 3 в пункт 4;

- участок, связывающий пункты 4 и 2.

Таким образом, в окончательном варианте цикл движения автомобиля принимает следующий вид:

t = {(2,1),(1,3),(3,4),(4,2)}.

Длина этого цикла будет равна:

l(t) = 2 + 2,5 + 3 + 1,5 = 9 км.

Далее необходимо сравнить длину полученного цикла l(t) с оценками неветвлённых подмножеств (рисунок 1).

ξ = 8

                                                             

					ξ = 9

 

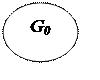
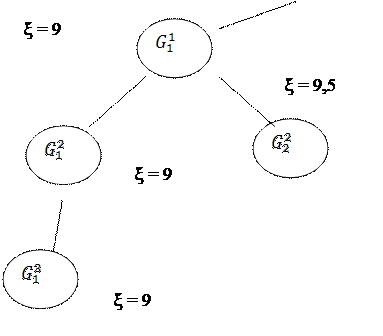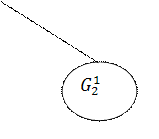Рисунок  1 - Дерево решений

Как видно из рисунка 1, имеется только два неветвлённых подмножества  и . В обоих случаях построенный цикл имеет меньшую оценку. Следовательно, предлагаемый цикл движения автомобиля является оптимальным. Его использование способно обеспечить сообщение с каждым пунктом при минимальном общем пробеге.