


 Допустим, в области Д
рассчитано статическое поле
Допустим, в области Д
рассчитано статическое поле ![]() по известным значениям
на границе, при условии, что заряды внутри Д отсутствуют.
по известным значениям
на границе, при условии, что заряды внутри Д отсутствуют.
В этом случае, в любой точке области Д поле Е удовлетворяет равенство:
![]()
Е – потенциально, значит
существует такой скаляр ![]() , для которого
, для которого
![]()
![]()
![]() -
теорема Тельмгольда.
-
теорема Тельмгольда.
С учетом этого предыдущее равенство получит вид:
![]()
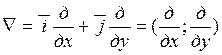 -оператор
Гомельтена.
-оператор
Гомельтена.
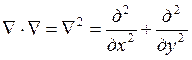 -оператор
Лапласа.
-оператор
Лапласа.
В результате для потенциала
![]() получается уравнение Лапласа или:
получается уравнение Лапласа или:
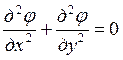
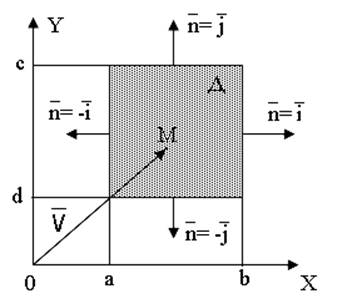
Для решения этого уравнения зададим граничные (краевые) условия.
На разных участках границы
должны быть известны либо потенциал ![]() , либо напряженность Е.
Согласно условию задаем напряженность, точнее
, либо напряженность Е.
Согласно условию задаем напряженность, точнее
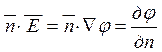 -производная
по направлению внешней нормали.
-производная
по направлению внешней нормали.
Т.о., должны быть использованы следующие краевые условия:
1) у=c, а≤х≤b, 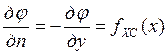 ;
;
2) у=d, а≤х≤b, 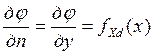 ;
;
3) x=a, c≤y≤d, 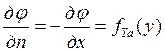 ;
;
4) x=b, c≤y≤d, 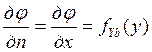 ;
;
Решение этой задачи примет вид двойного степенного ряда:
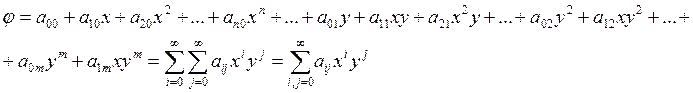
Вычислим необходимые производные от этой суммы:
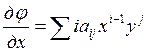
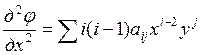
Во второй производной суммирование должно начинаться с i=2. Вместо i введем новый параметр: p=i-2, i=p+2.
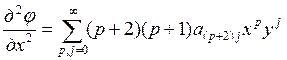 ;
;
Аналогично для ![]() :
: 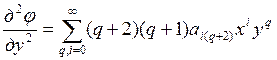
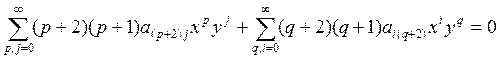
Сделаем переобозначение степеней:
![]() ;
; ![]() ;
;
В результате получим:
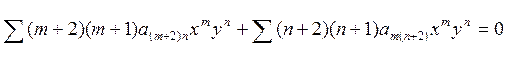
Равенство должно быть
верным при любых значениях х и у. Это обеспечивается обращением в ноль
коэффициентов перед ![]() в каждом из слагаемых. В
результате получаем систему уравнений для вычисления коэффициентов:
в каждом из слагаемых. В
результате получаем систему уравнений для вычисления коэффициентов:
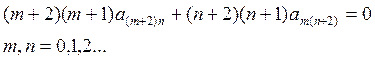
или:
![]()
![]()
![]()
![]()
Т.о. должны выполняться краевые условия:
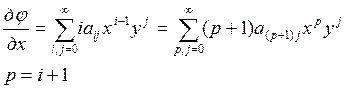
![]()
Эта производная задается при х=а и х=b, где:
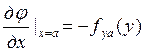
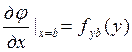
Для сопоставления этих выражений в производную сначала надо подставить х=а, а потом х=b, затем функцию в ряд по степеням у.
В результате получим равенство:![]()
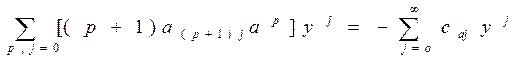
![]()
![]()
![]()
![]() -коэффициент.
-коэффициент.
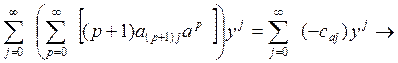 отсюда
следует бесконечная с-ма
отсюда
следует бесконечная с-ма
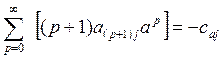
Аналогичные системы составляются для других сторон прямоугольника.
В результате для неизвестных ![]() получаем бесконечную систему линейных алгебраических
уравнений.
получаем бесконечную систему линейных алгебраических
уравнений.
Для решения этой системы необходимо
перейти от двойной нумерации неизвестных к одинарным ,т.е. вместо бесконечной
матрицы ![]() ,получаем матицу-вектор
,получаем матицу-вектор ![]() . Для этого нужно делать однозначный
переход .
. Для этого нужно делать однозначный
переход .
![]() Например,
следующим способом:
Например,
следующим способом:![]()
![]()
![]()
![]()
![]()
![]()
При решении системы всегда будут ограничения на число неизвестных , т.е. на размеры матрицы
Пусть
i =1,2; j=1,2![]() , тогда A= i +2 ( j – 1);
, тогда A= i +2 ( j – 1);
N=3 : A=i+3(j-1);
A=i+N(j-1)
В результате перенумерации
система приводится к следующему виду: ![]() =
=![]() , где А- бесконечная квадратная матрица
коэффициентов.
, где А- бесконечная квадратная матрица
коэффициентов.
![]()
![]() - векторы бесконечного пространства.
- векторы бесконечного пространства.
Доказывается, что решение существует и единственно, если все эти величины ограничены по норме, в качестве которой принимается:
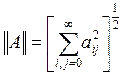
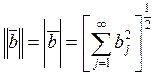
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.