




![]()
Каждому реальному вектору во взаимооднозначное соответствие можно поставить(при выбранном базисе) матрицу строку или матрицу столбик
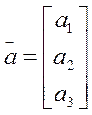 или
или ![]()
![]() или
или 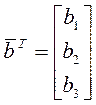
При этом базисные векторы имеют следующий вид:
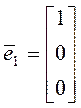 ;
; 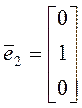 ;
; 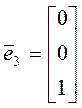 .
.
Тогда:
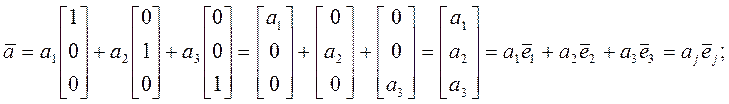
Аналогичное построение можно сделать для матриц любых размеров(плоских, кубических, n-мерных). В этом случае в качестве базиса пространства матриц используют диады, триады и т. д. базисных векторов.
Диада:
![]()
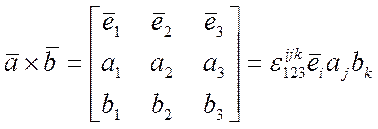
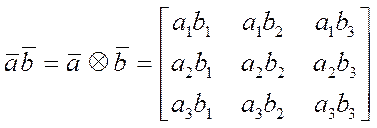
В соответствии с этим для базисных векторов:
![]()
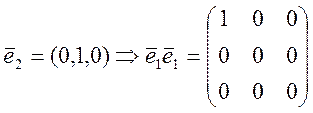
![]()
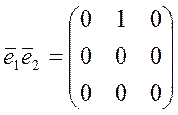 ;
; 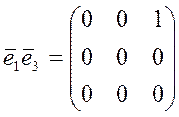 ;
; ![]()
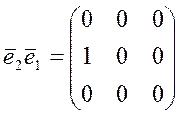 ;
;
С учетом этих представлений вводится понятие линейного оператора(Аффинор):
![]() - аффинор.
- аффинор.
![]()
где n - размерность.
Название(оператор)
связано с тем, что объект А преобразует вектор ![]() в
вектор
в
вектор ![]() по правилу:
по правилу: ![]() , при
этом функция
, при
этом функция ![]() обладает линейными свойствами:
обладает линейными свойствами:
1) ![]()
2) ![]()
Действия с линейным оператором. Свойства линейных операторов.
Оператор обладает всеми
свойствами вектора. Операторы образуют линейное пространство, значит в
определенных условиях их можно считать векторами. По этому, для каждого
оператора А, представленного в виде матрицы размером n на m в n – мерном пространстве ![]() ,
существует вектор
,
существует вектор ![]() - матрица строка или матрица
столбик, длинной
- матрица строка или матрица
столбик, длинной ![]() , принадлежащий
, принадлежащий ![]() и наоборот.
и наоборот.
Например: Пусть 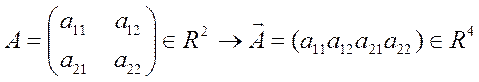
![]()
![]()
![]() где j=1,2,3,4,…
где j=1,2,3,4,…
![]() где I=i + 3( j - 1)
где I=i + 3( j - 1)
n=3
Пусть j=1, тогда:
![]()
![]()
![]() ;
; ![]() ;
;
![]() ;
; ![]() ;
; ![]() .
.
Правило перехода должно обеспечивать его взаимную однозначность. Описанное свойство операторов вытекает из свойств алгебраических действий сними.
1) Сложение: ![]() ;
; ![]() ;
;
![]() ;
; ![]() ;
; ![]() .
.
Если C=A+B, то должно быть:
![]()
Аналогично:
2) С=A·B; если ![]() ;
; ![]()
Рассмотрим как строится оператор С:
![]()
![]()
Где:
![]() .
.
Норма матрицы.
Норма матрицы не зависит от выбора координатной системы. Норма линейного оператора ( ||A|| ) – это числовая характеристика оператора, не зависящая от выбора координатной системы, в которой вычислена его матрица.
В различных ситуациях в качестве нормы могут быть приняты разные величины.
На пример:
![]() ;
; 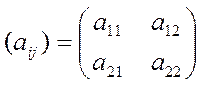 ;
;
1) ||A||=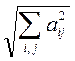 ;
;
2) ||A||=max(|![]() |);
|);
3) ||A||=max(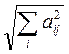 );
);
4) ||A||=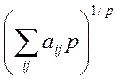 ;
;
…
Для матриц строк и столбцов, т.е. векторов, в качестве нормы чаще всего используют модуль.
Не зависимо от вида формулы, по которой считается норма, она должна удовлетворять следующим требованиям:
1) ||A|| > 0, A![]() 0;
0;
||A|| = 0, A=0.
2) ||A+B|| ![]() ||A|| +
||B||;
||A|| +
||B||;
3) ||AB|| = ||A|| ||B||;
4) ||kA|| = |k| ||A||, k![]() .
.
Двойная свертка оператора.
Рассмотренное выше произведение операторов еще сверткой по одному индексу. Наряду с этим используется двойная сетка, т.е. свертка по двум индексам.
![]()
![]() .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.