ЗАДАЧА ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ № 4
Условие задачи:
Четыре ЛДК производят материалы для мебельных фабрик. Соответственно на каждую фабрику рассчитано определенное количество сырья. Требуется составить оптимальный план перевозок, то есть указать, сколько груза должен получить потребитель от каждого поставщика. При этом необходимо вывести весь груз из пунктов отправления, удовлетворить все заявки потребителей и обеспечить минимум затрат на перевозку всего груза.
Используемые данные:
Таблица 4.1
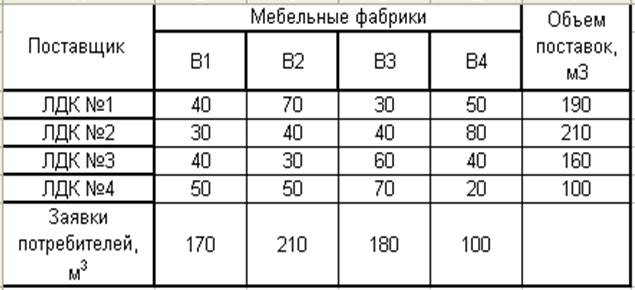
Решение:
Необходимо построить математическую модель.
Переменными в модели будет являться стоимость перевозки единицы груза потребителю (в руб.) мебельных фабрик В1, В2, В3, В4. Математическая модель задачи линейного программирования включает целевую функцию и ограничения.
Целевая функция обозначается Z и находится по формуле:
Z = E17+D17+C17+B17 min (4)
При решении данной задачи необходимо учесть ограничения на расход исходных продуктов и на спрос.
Ограничения:
$B$12:$E$15 >= 0
$B$7:$E$7 = $B$16:$E$16
$F$3:$F$6 <= $F$12:$F$15
Таблица 4.2
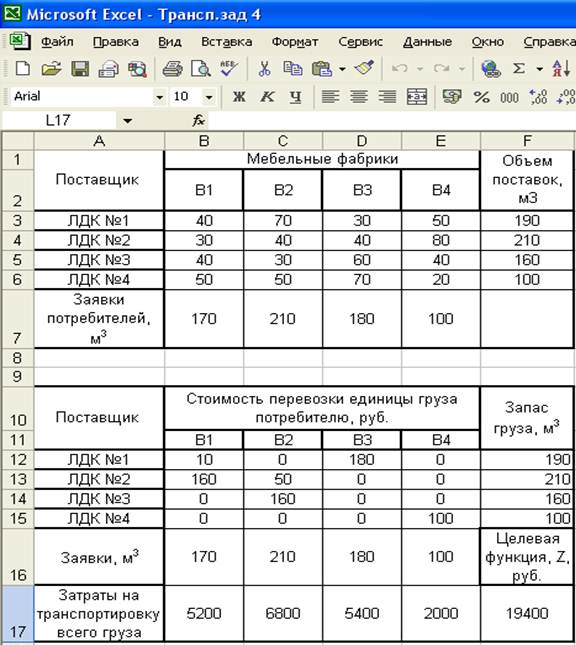
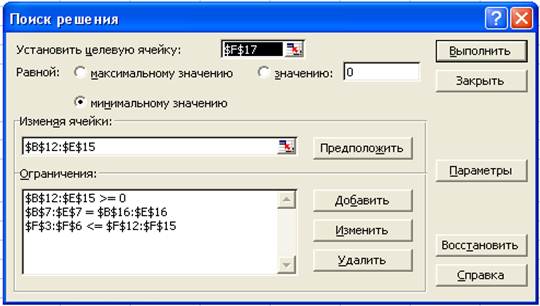 |
Рис. 4.1
Вывод: оптимальный план перевозок составляет – ЛДК №1 поставляет 1-ой фабрике 10, 3-ей – 180 материалов, ЛДК №2 – 1-ой 160,2-ой 50, ЛДК №3 – 2-ой 160, ЛДК №4 – 4-ой 100.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.