F- число Фарадея.
Приклади розв'язування задач
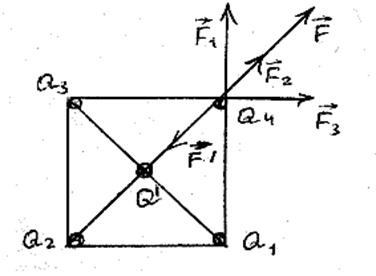
Приклад 1. У вершинах квадрата з стороною «а» знаходяться однакові однойменні заряди «Q». Який заряд «Q1» протилежного знаку необхідно помістити в центрі квадрата, щоб діюча на будь - який із зарядів сила дорівнювала нулю?
Дано: Q1=Q2 =Q3 = Q4 = Q
Розв’язання
Для визначення заряду «Q1» використаємо закон Кулона. Розглянемо сили, що діють на будь - який із зарядів «Q», розміщених в одній з вершин квадрата з боку решти однойменних зарядів «Q». Позначимо ці сили відповідно через F1=F3 i F2, Напрями цих сил показано на рис.8.
|
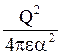 і
F2 =
і
F2 = 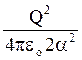 , тому що відстань між зарядами Q2 i Q4 дорівнює
, тому що відстань між зарядами Q2 i Q4 дорівнює
F =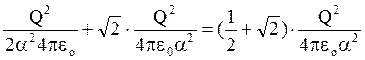
![]()
Вона повинна
дорівнювати силі F1 = 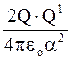 , що діє на розглянутий заряд з боку заряду Q1.
, що діє на розглянутий заряд з боку заряду Q1.
Прирівнявши праві частини останніх рівнянь, дістанемо
Q1 = 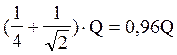
Тобто величина заряду Q1 залежить лише від величини заряду «Q» і зовсім не залежить від розмірів сторони квадрата.
Приклад 2. Два однакових позитивних заряди 10-7Кл знаходяться в повітрі на відстані 8 см один від одного. Визначити напруженість поля в точці 0, яка знаходиться на середині відстані між зарядами і в точці А, що лежить на відстані 5 см від зарядів.
Дано: Q1 =Q2 = 10-7 Кл; e = 1, r = 0,08 м, r1 = 0,05м.
Знайти: Ео і ЕА
Розв’язання
Напруженість поля, створюваного зарядами, знаходиться за принципом суперпозиції.
Щоб знайти значення
напруженості в точці 0, треба спочатку намалювати вектори напруженості полів.
Для позитивних зарядів вектори напруженості напрямлені по одній прямій в
протилежні сторони. Крім того, ці заряди рівні і лежать на рівних відстанях від
точки 0, значить результуюча напруженість ![]() .
Тепер намалюємо вектори
.
Тепер намалюємо вектори
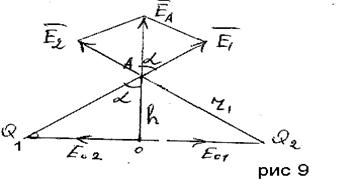 напруженості полів
напруженості полів ![]() в точці А. Результуючий вектор
напруженості
в точці А. Результуючий вектор
напруженості ![]() є діагоналлю паралелограма, тобто
є діагоналлю паралелограма, тобто ![]() , або ЕА = 2Е1cosa, тому що Е1 і Е2 рівні між
собою.
, або ЕА = 2Е1cosa, тому що Е1 і Е2 рівні між
собою.
Напруженість визначається за формулою
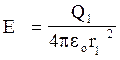
Тригонометричну
функцію cos a знайдемо за умовою cosa =![]() , тоді числове значення напруженості поля в
точці А визначиться за формулою
, тоді числове значення напруженості поля в
точці А визначиться за формулою
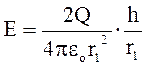 ,
,
ЕА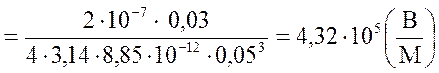
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.