Загальні пояснення та рекомендації до виконання індивідуальної роботи з дисципліни «Вища математика»

Глава V.  ІНДИВІДУАЛЬНЕ ДОМАШНЄ ЗАВДАННЯ № 2

З ДИСЦИПЛІНИ “ВИЩА МАТЕМАТИКА» ДЛЯ СТУДЕНТІВ ЗАОЧНОЇ ФОРМИ НАВЧАННЯ ТА РЕКОМЕНДАЦІЇ ДО ЙОГО ВИКОНАННЯ

§1. ЗАГАЛЬНІ ПОЯСНЕННЯ ТА РЕКОМЕНДАЦІЇ

ДО ВИКОНАННЯ ІНДИВІДУАЛЬНОЇ РОБОТИ

Індивідуальна робота містить завдання з розділів «Дослідження функцій та побудова їх графіків», «Інтегральне числення»,  «Диференціальні рівняння» та «Ряди».

Основні вимоги до виконання роботи:

-  самостійність виконання;

-  своєчасність надсилання роботи;

-  відповідність номера варіанта, в противному разі робота буде повернена на повторне виконання;

-  робота повинна бути виконана повністю;

-  завдання треба розташовувати по порядку за номерами, що вказані в завданні, із збереженням нумерації;

-  кожне завдання необхідно оформити за такою схемою: умова завдання (переписати у відповідності до свого варіанта); розв’язання задач (має бути обґрунтованим, з наведенням формул, назв відповідних теорем, відомих фактів, якими користувалися); відповідь (повна);

-  роботу треба виконати в окремому зошиті з полями для зауважень викладача, інтервалами між рядками, без скорочень, розбірливим почерком;

-  наприкінці роботи наводиться список літератури, ставиться дата її виконання, підпис студента, залишається місце для рецензії.

Якщо в роботі допущені помилки, не всі відповіді розкривають зміст питань, вона не зараховується і повертається студенту для доопрацювання (в тому ж зошиті). Роботи, що виконані не самостійно, неохайно, нерозбірливим почерком, а також не за встановленим варіантом, повертаються без перевірки.

Завдання для роботи містять 5 варіантів. Номер варіанта залежить від початкової букви прізвища студента.

§2. ЗАВДАННЯ ІНДИВІДУАЛЬНОЇ РОБОТИ

Варіант № 1

1.Дослідити функцію на монотонність та екстремуми: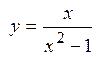

2. Дослідити на екстремум функцію

3. Знайти невизначені інтеграли :

а) 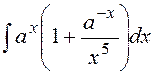 б) 

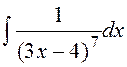
в)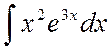

4. Обчислити визначені інтеграли :

а) 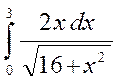                                 б)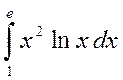

5. Обчислити площу фігури, обмежену лініями :

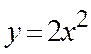              і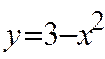        

6. Розв’язати задачу економічного змісту:

Функція маргінального доходу підприємства має вигляд 10-0,02x (у гривнях), де  - кількість одиниць продукції. Знайти зміну загального доходу, якщо виробництво зросте з 20 до 40 одиниць.

7. Дослідити на екстремум функцію двох змінних:

8. Розв”язати диференціальні рівняння:

1)

2)

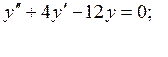
9. Знайти область збіжності степеневого ряду:

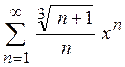
Варіант № 2

1.  Знайти найбільше та найменше значення функції  на відрізку  [-2;1].

2.   Експериментально отримані п’ять значень функції y = f(x) при п’яти значеннях аргументу, які записані в таблиці.

Методом найменших квадратів знайти функцію Y = ax + b, яка виражає приблизно (апроксімує) функцію y = f(x). Зробити рисунок, на якому в декартовій прямокутній системі координат побудувати експериментальні точки і графік функції Y = ax + b, що апроксімує

3. Знайти невизначені інтеграли :

а) 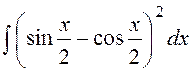 б)

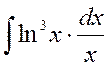
в)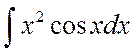

4. Обчислити визначені інтеграли :

а) 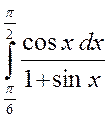                                   б)

5. Обчислити площу фігури, обмежену лініями :

                і        

6.  Розв’язати задачу економічного змісту:

Функція маргінальних витрат підприємства має вигляд 100-4x (у гривнях), де  - кількість виготовлених виробів. Знайти зростання загальних витрат, коли виробництво зростає з 10 до 20 одиниць.

7. Дослідити на екстремум функцію двох змінних:

8. Розв”язати диференціальні рівняння:

1)

2)

9. Знайти область збіжності степеневого ряду:

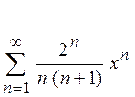
Варіант № 3

1.   Дослідити функцію на монотонність та екстремуми: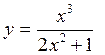

2.  Дослідити на екстремум функцію

3.  Знайти невизначені інтеграли :а) 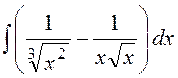  б)

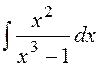
в)

4.  Обчислити визначені інтеграли :

а) 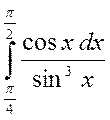                                  б)

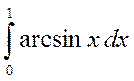
5.  Обчислити площу фігури, обмежену лініями :

            і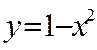        

6.  Розв’язати задачу економічного змісту:

Функція маргінального прибутку підприємства має вигляд 70-0,2x (у гривнях), де  - кількість одиниць продукції. Знайти зміну загального прибутку, якщо виробництво зросте з 10 до 20 одиниць.

7.  Дослідити на екстремум функцію двох змінних:

8.  Розв’язати диференціальні рівняння:

1)

2)

9. Знайти область збіжності степеневого ряду:

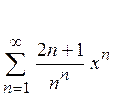
Варіант № 4

1. Знайти найбільше та найменше значення функції  на відрізку [0;1].

2. Дослідити на екстремум функцію

3. Знайти невизначені інтеграли :

а) 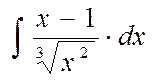 б)

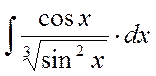
в)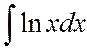

4. Обчислити визначені інтеграли :

а) 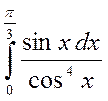                                   б)

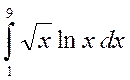
5. Обчислити площу фігури, обмежену лініями :

                   і        

6. Розв’язати задачу економічного змісту:

Функція маргінального доходу підприємства має вигляд 12-0,2x (у гривнях), де  - кількість одиниць продукції. Знайти зміну загального доходу, якщо виробництво зросте з 20 до 30 одиниць.

7. Дослідити на екстремум функцію двох змінних:

8. Розв’язати диференціальні рівняння:

1)    2)

9. Знайти область збіжності степеневого ряду:

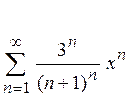
Варіант № 5

1.  Дослідити функцію на монотонність та екстремуми: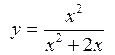

2.   Експериментально отримані п’ять значень функції y = f(x) при п’яти значеннях аргументу, які записані в таблиці.

Методом найменших квадратів знайти функцію Y = ax + b, яка виражає приблизно (апроксімує) функцію y = f(x).Зробити рисунок, на якому в декартовій прямокутній системі координат побудувати експериментальні точки і графік функції Y = ax + b, що апроксімує дану.

3. Знайти невизначені інтеграли :

а) 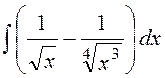  б)

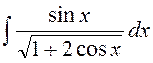
в)

4. Обчислити визначені інтеграли :

а) 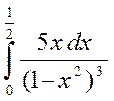                                  б)

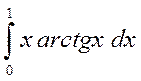
5. Обчислити площу фігури, обмежену лініями :

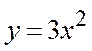              і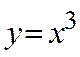        

6. Розв’язати задачу економічного змісту:

Функція маргінальних витрат підприємства має вигляд 100-2x (у гривнях), де x - кількість виготовлених виробів. Знайти зростання загальних витрат, коли виробництво зростає з 20 до 40 одиниць.

7. Дослідити на екстремум функцію двох змінних:

8. Розв’язати диференціальні рівняння:

1)

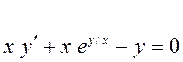
2)

9. Знайти область збіжності степеневого ряду:

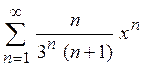
§ 3. ОСНОВНІ ТЕОРЕТИЧНІ ВІДОМОСТІ ДО ЗАВДАННЯ № 1, 2

Дослідження функцій та побудова їх графіків

Схема дослідження функції на монотонність та екстремуми

1) D(y);

2) y´;

3) знайти критичні точки;

4) визначити проміжки знакосталості y´Þвстановити проміжки монотонності y;

5) прослідкувати за зміною знака y´ при переході через критичні точки Þ встановити точки екстремуму.

Достатня ознака монотонності

Точка x₀називається точкою максимуму функції  f(x), якщо  f(x0) – найбільше значення функції  f(x) в деякому околі точки x0 .

Точка x₀з області визначення функції  f(x) називається критичною точкою функції  f(x), якщо  f´(x₀)=0   або  f´(x₀) не існує .

Достатня ознака екстремуму

Якщо f´(x)при переході через критичну точку x₀ змінює свій знак на протилежний, то x₀ – точка екстремуму.

Схема розв´язання задачі на знаходження найбільшого та найменшого значення функції f(x) на відрізку [a;b] 

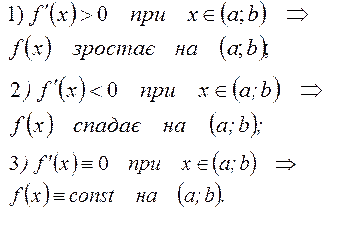
1)  знайти D(y), перевірити, що [a;b] є D(y);

2)  -?;

3)  знайти критичні точки функції f(x);

4)  обрати ті з них, що належать [a;b];

5)  обчислити значення f(x) в обраних критичних точках та на кінцях