Методичні рекомендації до практичних занять з дисципліни «Вища математика»

Глава ІІ.МЕТОДИЧНІ РЕКОМЕНДАЦІЇ ДО ПРАКТИЧНИХ ЗАНЯТЬ З ДИСЦИПЛІНИ «ВИЩА МАТЕМАТИКА»

Розділ 9. ДОСЛІДЖЕННЯ ФУНКЦІЙ ТА ПОБУДОВА ЇХ ГРАФІКІВ

Основні питання, що виносяться на практичні заняття за

Розділом 9:

1.Дослідження функції на монотонність та екстремуми.

2.Дослідження функції на опуклість, угнутість.

3.Знаходження асимптот функції.

4.Схема дослідження функції та побудови її графіка.

5.Знаходження найбільшого та найменшого значення функції на відрізку.

6.Знаходження екстремумів функції двох змінних за допомогою необхідних і достатніх умов екстремуму.

7.Застосування методу найменших квадратів (на економічних прикладах).

8.Знаходження умовного екстремуму функції методом Лагранжа.

Після опрацювання розділу на практичних заняттях студент повинен

знати: достатні ознаки монотонності, екстремуму, опуклості, угнутості, точок перегину графіка функції однієї змінної; формули для знаходження рівняння похилої асимптоти графіка функції однієї змінної; схему дослідження функції та побудови її графіка; алгоритм знаходження найбільшого та найменшого значення функції однієї змінної на відрізку; необхідні і достатні умови екстремуму функції двох змінних; метод найменших квадратів; метод Лагранжа для знаходження умовного екстремуму функції багатьох змінних.

вміти: досліджувати функцію на монотонність та екстремуми, на на опуклість, угнутість, точки перегину; знаходити вертикальні та похилі асимптоти графіка функції; здійснювати повне дослідження функції та будувати її графік; знаходити найбільше та найменше значення функції на відрізку; знаходити екстремуми функції двох змінних за допомогою необхідних і достатніх умов екстремуму; застосовувати метод найменших; знаходити умовний екстремум функції методом Лагранжа.

Рекомендована література:

[1], т. І, с. 220-232.

[2], с. 457-472.

[3], с. 262-270.

Рекомендації до розв’язання типових прикладів розділу 9:

9.1. Дослідити на монотонність і екстремуми функцію  y=3x³+4,5x²-4x+1.

Розв’язання.  D(y)=(-∞;+∞),

y′=9x²+9x-4=(3x-1)(3x+4),

y′=0: x= -D(y),  x=D(y) – критичні точки функції.

 

Відповідь: функція зростає при x(-∞; -) та при  x(;  +∞), функція спадає при x( -; );

x= - - точка максимуму, x= - точка мінімуму.

9.2. Дослідити на екстремум функцію

Розв’язання. Функція визначена при . Знайдемо похідну:  при 1-2х²=0; звідки  (стаціонарні точки);  при , тобто на межах області визначення функції.

Знайдемо другу похідну: . Обчислимо значення другої похідної у стаціонарних точках. При   маємо

,

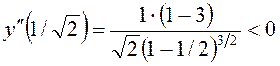Отже, робимо висновок, що в точці  функція має максимум . При  одержимо

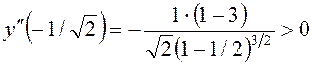, тобто в точці  функція має мінімум .

У критичних точках  екстремум немає, так як за визначенням точками екстремуму можуть бути лише внутрішні точки області визначення функції.

9.3. Знайти найбільше і найменше значення функції  на відрізку [-2, 3].

Розв’язання. Знаходимо похідну: , тобто  - стаціонарні точки. Визначаємо значення функції в цих точках:  Обчислюємо значення даної функції на межах проміжку:  З одержаних чотирьох значень вибираємо найбільше і найменше.

Отже, найбільше значення функції на даному відрізку дорівнює 2, а найменше дорівнює -18.

9.4. Дослідити на опуклість функцію .

Розв’язання. Маємо , . Якщо х<0, то  і крива опукла; якщо ж х>0, то  і крива угнута. Отже, крива опукла в проміжку  і угнута в проміжку .

9.5. Знайти екстремуми функції  і точки перегину її графіку.

Розв’язання. Знайдемо першу похідну:  Корені першої похідної: х₁=-1, х₂=1. Знайдемо другу похідну: . Обчислимо значення другої похідної в стаціонарних точках:  тобто , тобто .

Знайдемо точку перегину, для чого другу похідну прирівняємо нулю: 6х=0, тобто х=0. Зліва від точки  х=0 маємо   – крива опукла, а праворуч від точки  х=0 маємо – крива угнута; отже, точка з абсцисою х=0  є точкою перегину; .

9.6. Знайти точки перегину кривої .

Розв’язання. Знаходимо

,         .

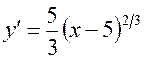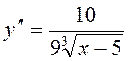Друга похідна не дорівнює нулю ні при яких значеннях х і не існує в точці . х=5. Значення х=5 є абсцисою точки перегину, так як , . Таким чином, (5; 2) – точка перегину.

9.7. Побудувати графік функції .

Розв’язання. 1) Область визначення функції – вся вісь Ох за винятком точки х=0, тобто 

2) Функція не є парною або непарною.

3) Знайдемо точки перетину графіка з віссю Ох; маємо ; .

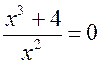4) Точка розриву х=0,причому  отже, х=0 (вісь Oy) є вертикальною асимптотою графіка.

Знайдемо похилі асимптоти:

;

.

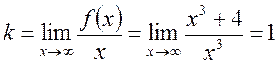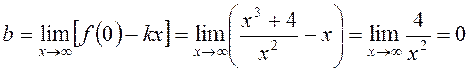Похила асимптота має рівняння y=x.

5) Знайдемо екстремуми функції і інтервали зростання і убування. Маємо  при х=2;  при х=0 (точка розриву функції).

Точки х=0 і  х=2 розбивають числову вісь на проміжки