міститься зайва інформація в підкресленій умові задачі: „Чи існує двозначне число, яке при діленні на суму квадратів його цифр дає в частці 2 і в залишку 6, а при діленні на добуток його цифр дає в частці 4 і в залишку 6?”
Вiдповiдь: так.
Розв’язання..
Нехай ![]() - цифра десятків (
- цифра десятків (![]() ),
),
![]() - цифра одиниць шуканого двозначного числа.
Тоді воно має вигляд
- цифра одиниць шуканого двозначного числа.
Тоді воно має вигляд ![]() .
Якщо відкинути підкреслену умову, то невідомі
.
Якщо відкинути підкреслену умову, то невідомі ![]() і
і![]() задовольнятимуть рівняння
задовольнятимуть рівняння ![]() або
або 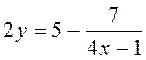 .
.
Оскільки ![]() , то це рівняння має єдиний цілий розв’язок:
, то це рівняння має єдиний цілий розв’язок: ![]() .
.
Однак, неважко перевірити, що число 22 не задовольняє умові задачі з відкинутою інформацією. Отже, не існує двозначного числа, яке задовольняє умові, яка залишилася, тим більш не існує такого числа з будь-якою додатковою інформацією.
Це означає, що підкреслена інформація є зайвою.
Задачі на функції
1. Довести, що функція ![]() є періодичною, якщо існує
є періодичною, якщо існує ![]() таке,
що для будь – якого
таке,
що для будь – якого![]()
![]() ,
,![]() та виконується умова
та виконується умова
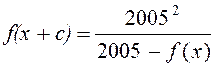 .
.
Доведення.
![]()
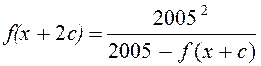
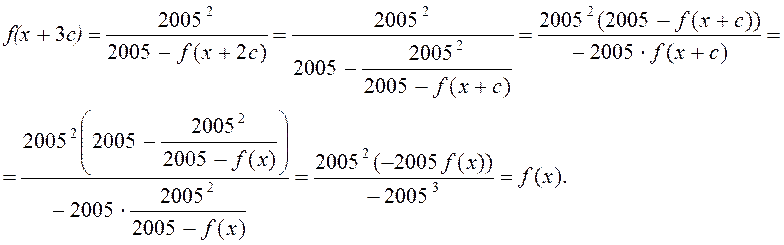
2. Знайти всі функції
![]() , для яких при будь-яких
, для яких при будь-яких ![]() виконується рівність:
виконується рівність:
![]() .
.
Відповідь: ![]()
Розв΄язання.
Виконаємо послідовно
заміни ![]() ;
;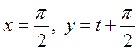 ;
; 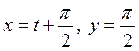 . Тоді дістанемо систему рівнянь:
. Тоді дістанемо систему рівнянь:
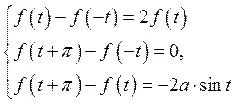 , де
, де 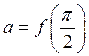 .
.
Звідси ![]() або
або ![]() , де
, де ![]()
Перевірка показує, що
знайдена функція є розв΄язком даної задачі для будь-якого дійсного ![]() .
.
3. Знайти всі
неперервні функції ![]() , для яких при будь-яких дійсних
, для яких при будь-яких дійсних ![]() виконується рівність
виконується рівність 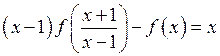 .
.
Відповідь: ![]() .
.
Розв΄язання.
Нехай 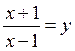 , тоді
, тоді 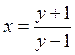 , і
рівняння набирає вигляду
, і
рівняння набирає вигляду 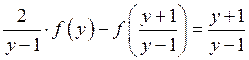 .
.
Таким чином, для
знаходження функції ![]() маємо систему двох рівнянь:
маємо систему двох рівнянь:
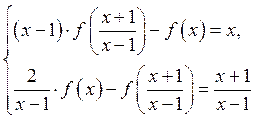 .
.
Помножимо обидві
частини другого рівняння на ![]() і додамо до першого
рівняння. Тоді дістанемо:
і додамо до першого
рівняння. Тоді дістанемо: ![]() ,
, ![]() . Внаслідок неперервності шуканої функції
остаточно маємо:
. Внаслідок неперервності шуканої функції
остаточно маємо: ![]()
![]() .
.
4. Многочлен ![]() з цілими коефіцієнтами дорівнюе 5 при
з цілими коефіцієнтами дорівнюе 5 при ![]() и
и ![]() . Чи існує ціле число
. Чи існує ціле число ![]() , при якому
цей многочлен дорівнює 6?
, при якому
цей многочлен дорівнює 6?
Вiдповiдь: нi.
Розв’язання.
З умови задачi
випливає, що ![]() i
i ![]() є коренi
многочлена
є коренi
многочлена![]() .
.
Тому
![]() =
=![]() (1), де
(1), де ![]() -
многочлен с цiлими коефiцiєнтами.
-
многочлен с цiлими коефiцiєнтами.
Якщо iснує цiле
число ![]() таке, що
таке, що ![]() , то з
формули(1) маємо
, то з
формули(1) маємо
![]() .
.
Але це неможливо, оскiльки одиницю не можна подати у виглядi добутка чотирьох цiлих множникiв, принаймнi три з якiх рiзнi.
Отже, не iснує цiлого x, про яке iде мова в задачi.
5. Знайти всі функції![]() , які при будь-яких дійсних
, які при будь-яких дійсних ![]() задовольняють рівняння
задовольняють рівняння ![]() .
.
Відповідь: таких функцій не існує.
Розв’язання .
Підставляючи ![]() в дане функціональне рівняння, дістаємо
в дане функціональне рівняння, дістаємо
![]() . Це рівняння має два дійсних корені
. Це рівняння має два дійсних корені ![]() або
або ![]() .
Покладаючи
.
Покладаючи ![]() у функціональному рівнянні, маємо
у функціональному рівнянні, маємо ![]() або
або ![]() .
.
Якщо ![]() , то
, то ![]() .
.
Якщо ![]() , то
, то ![]() .
.
Перевірка показує, що жодна знайдена функція не задовольняє вихідне функціональне рівняння, отже це рівняння не має розв’язків.
6. Знайти всі функції![]() , які при будь-яких дійсних
, які при будь-яких дійсних ![]() задовольняють рівняння
задовольняють рівняння ![]() .
.
Відповідь: ![]() .
.
Розв’язання .
Підставляючи ![]() в дане функціональне рівняння, дістаємо
в дане функціональне рівняння, дістаємо![]() .
.
Це рівняння має
єдиний дійсний корінь ![]() . Покладаючи
. Покладаючи ![]() у функціональному рівнянні, маємо
у функціональному рівнянні, маємо ![]() , звідки, з урахуванням рівності
, звідки, з урахуванням рівності ![]() , дістаємо
, дістаємо ![]() .
.
Перевірка показує, що
функція ![]() задовольняє вихідне функціональне
рівняння, а тому є єдиним його розв’язком.
задовольняє вихідне функціональне
рівняння, а тому є єдиним його розв’язком.
7. Знайти всі функції![]() , які при будь-яких дійсних
, які при будь-яких дійсних ![]() задовольняють рівняння
задовольняють рівняння ![]() .
.
Відповідь: 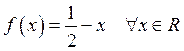 .
.
Розв’язання .
Якщо у функціональне
рівняння підставити![]() , то дістанемо рівняння
, то дістанемо рівняння ![]() або
або ![]() .
Покладаючи в цьому рівнянні
.
Покладаючи в цьому рівнянні ![]() , дістаємо
, дістаємо ![]() , тобто
, тобто 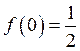 . Отже,
. Отже,
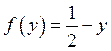 , тобто
, тобто 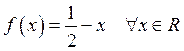 .
.
Перевірка показує, що
функція 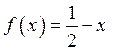 задовольняє умову задачі.
задовольняє умову задачі.
8. Функція ![]() задовольняє умови:
задовольняє умови: 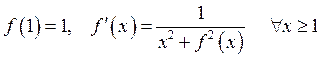 .
Довести, що існує
.
Довести, що існує ![]() і що ця границя не більше, ніж
і що ця границя не більше, ніж ![]() .
.
Доведення.
З умови задачі
випливає , що ![]()
![]() , а це
означає, що функція
, а це
означає, що функція ![]() зростає на проміжку
зростає на проміжку ![]() . Крім того, з умови задачі також випливає,
що
. Крім того, з умови задачі також випливає,
що 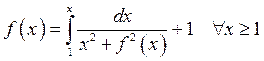 . А це означає, що
. А це означає, що 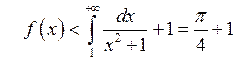 ,
оскільки
,
оскільки ![]() .
.
Таким чином, функція
![]() є зростаючою і обмеженою зверху числом
є зростаючою і обмеженою зверху числом ![]() , а це означає, що згідно з теоремою
Вейєрштраса
, а це означає, що згідно з теоремою
Вейєрштраса ![]() має при
має при ![]() скінчену
границю і ця границя не більше, ніж
скінчену
границю і ця границя не більше, ніж ![]() , що й треба було
довести.
, що й треба було
довести.
9. Нехай многочлен ![]() степеня
степеня ![]() з
дійсними коефіцієнтами при всіх дійсних значеннях
з
дійсними коефіцієнтами при всіх дійсних значеннях ![]() набуває
лише додатних значень. Довести, що многочлен
набуває
лише додатних значень. Довести, що многочлен ![]() можна
подати у вигляді суми квадратів двох многочленів.
можна
подати у вигляді суми квадратів двох многочленів.
Доведення.
З умови задачі
випливає, що ![]() - многочлен парного степеня (
- многочлен парного степеня (![]() ), коефіцієнт при старшому степені більше
за 0 ( можна вважати, що він дорівнює 1) і що всі корені многочлена
), коефіцієнт при старшому степені більше
за 0 ( можна вважати, що він дорівнює 1) і що всі корені многочлена ![]() комплексно спряжені:
комплексно спряжені: ![]() і
і ![]() ,
, ![]() і
і ![]() , …,
, …, ![]() и.
и. ![]() . Отже,
многочлен
. Отже,
многочлен ![]() можна подати у вигляді:
можна подати у вигляді: ![]() . Добуток перших
. Добуток перших ![]() множників
є многочлен степеня
множників
є многочлен степеня ![]() . Цей многочлен є комплексно
спряженим до многочлена степеня
. Цей многочлен є комплексно
спряженим до многочлена степеня ![]() , що дорівнює добутку
останніх
, що дорівнює добутку
останніх ![]() множників, тобто
множників, тобто ![]() або
або
![]() , що й треба було довести.
, що й треба було довести.
Задачі на границі
1. Для всіх значень
дійсного параметра ![]() роз΄язати
рівняння:
роз΄язати
рівняння:
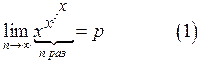 .
.
Відповідь: якщо ![]() , те
, те ![]() ; якщо
; якщо ![]() , те
, те ![]() .
.
Розв΄язання.
Розглянемо
послідовність 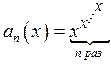 . Тоді
. Тоді ![]() .
.
Припустимо, що
рівняння ![]() має розв΄язок.
Переходячи в рівності
має розв΄язок.
Переходячи в рівності ![]() до границі при
до границі при ![]() дістаємо:
дістаємо: ![]() , звідки
, звідки
![]() .
.
Таким чином, якщо
рівняння ![]() має розв΄язок,
то
має розв΄язок,
то ![]() .
.
З'ясуємо, при яких ![]() послідовність
послідовність 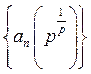 збігається
і має границю, яка дорівнює
збігається
і має границю, яка дорівнює ![]() .
.
Оскільки ![]() , то
, то ![]() ,
, ![]() ,...,
,..., 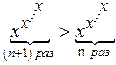 і,
отже,
і,
отже, ![]() , тобто послідовність
, тобто послідовність 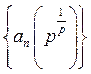 зростає.
зростає.
За допомогою метода
математичної індукції неважко також довести, що 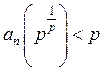 .
Дійсно,
.
Дійсно, 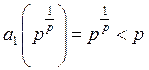 , тому що
, тому що ![]() . Якщо ж
припустити, що
. Якщо ж
припустити, що 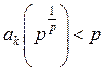 , то і
, то і 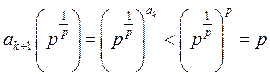 .
.
Таким чином,
послідовність 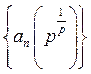 обмежена зверху. Тому за
теоремою Вейерштрасса послідовність
обмежена зверху. Тому за
теоремою Вейерштрасса послідовність 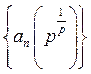 має скінчену границю
має скінчену границю ![]() . Підставляючи
. Підставляючи ![]() в
рівність
в
рівність ![]() і переходячи до границі при
і переходячи до границі при ![]() , дістаємо, що
, дістаємо, що ![]() є
коренем рівняння
є
коренем рівняння ![]()
![]() , де
, де 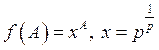 .
.
Рівняння ![]()
![]() має корінь
має корінь ![]() , причому
, причому ![]() .
.
Розглянемо 3 випадка.
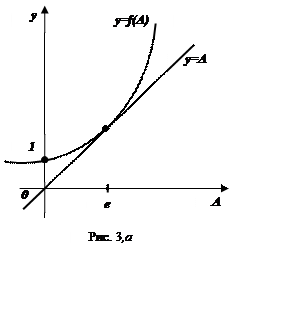
1).Якщо ![]() , то
, то ![]() й отже
рівняння
й отже
рівняння ![]() має єдиний розв’язок
має єдиний розв’язок ![]() (пряма
(пряма ![]() є
дотичною до графіка показникової функції
є
дотичною до графіка показникової функції ![]() в точці
в точці
![]() ) (рис.3а).
) (рис.3а).
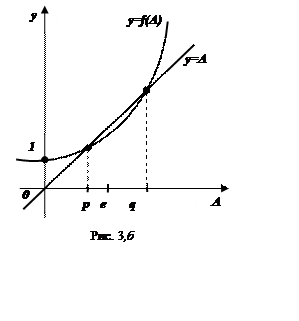
2).Якщо ![]() , то
, то ![]() і
рівняння
і
рівняння ![]() має два корені:
має два корені: ![]() і
і
![]() . Оскільки
. Оскільки 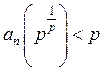 , то
, то ![]() (рис.3б).
(рис.3б).
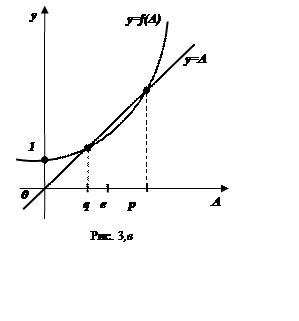
3).Якщо ![]() , то
, то ![]() і
рівняння
і
рівняння ![]() має два корені:
має два корені: ![]() і
і
![]() (рис.3в). При цьому
(рис.3в). При цьому 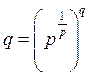 , звідки
, звідки ![]() . Тому
. Тому 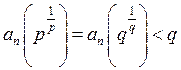 . Отже, у цьому випадку
. Отже, у цьому випадку ![]() .
.
Таким чином, 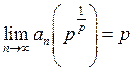 , якщо
, якщо ![]() і
і 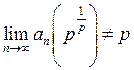 , якщо
, якщо ![]() .
.
Отже, якщо ![]() , то рівняння має єдиний розв΄язок
, то рівняння має єдиний розв΄язок
![]() ; а якщо
; а якщо ![]() , то
рівняння не має розв΄язків.
, то
рівняння не має розв΄язків.
2. Послідовність ![]() ,
, ![]() задано
за допомогою рекурентної формули :
задано
за допомогою рекурентної формули : ![]() ,
, ![]() . Знайти
. Знайти 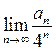 .
.
Відповідь: ![]() .
.
Розв’язання .
Перший спосіб.
З умови задачі випливає, що
![]() ,
, ![]()
![]() ,
,
![]() …
…
або
![]() ,
,
![]() ,
,
![]() …
…
Припустимо, що ![]() . Використовуючи формулу для суми
. Використовуючи формулу для суми ![]() перших членів геометричної прогресії,
дістаємо формулу
перших членів геометричної прогресії,
дістаємо формулу
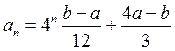 , яку неважко довести
за допомогою метода математичної індукції.
, яку неважко довести
за допомогою метода математичної індукції.
Таким чином, 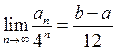 .
.
Другий спосіб.
Рекурентну формулу ![]() , тобто
, тобто ![]() , можна
записати у вигляді
, можна
записати у вигляді ![]() або у вигляді
або у вигляді ![]() . Звідси випливає, що
. Звідси випливає, що
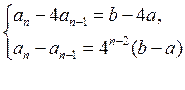 .
.
Виключаючи із цієї
системи ![]() , дістаємо:
, дістаємо: 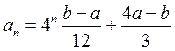 .
Тому
.
Тому 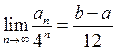 .
.
3. Послідовність ![]() ,
, ![]() задано
за допомогою рекурентної формули :
задано
за допомогою рекурентної формули : ![]() ,
,![]() . Знайти
. Знайти 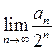 .
.
Відповідь: ![]() .
.
Розв’язання .
Перший спосіб.
З умови задачі випливає, що
![]() ,
, ![]()
![]() ,
,
![]() …
…
або
![]() ,
,
![]() ,
,
![]() …
…
За допомогою метода
математичної індукції неважко довести, що ![]() . Цю
формулу можна перетворити до вигляду
. Цю
формулу можна перетворити до вигляду 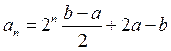 , звідки випливає, що
, звідки випливає, що 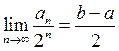 .
.
Другий спосіб.
Рекурентну формулу ![]() ,т. е
,т. е ![]() ,
можна записати у вигляді
,
можна записати у вигляді ![]()
![]() або
у вигляді
або
у вигляді ![]() . Звідси випливає, що
. Звідси випливає, що
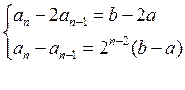 .
.
Виключаючи із цієї
системи ![]() , дістаємо:
, дістаємо: 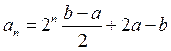 . Тому
. Тому
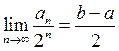 .
.
4. Які числові
значення може набувати 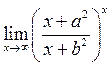 , якщо
, якщо ![]() ?
?
Відповідь: будь-яке
значення з відрізку 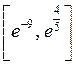 .
.
Розв’язання .
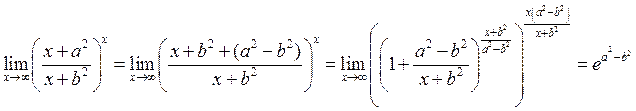 .
.
З нерівності ![]() випливає, що
випливає, що 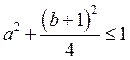 .
Знайдемо найбільше й найменше значення функції
.
Знайдемо найбільше й найменше значення функції ![]() в
області
в
області 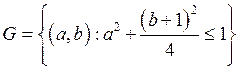 . Усередині області
. Усередині області ![]() існує
єдина стаціонарна точка
існує
єдина стаціонарна точка ![]() , причому
, причому ![]() . На границі
. На границі ![]() області
області ![]() маємо
маємо 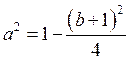 ,
отже
,
отже 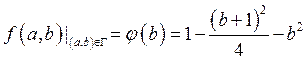 , де
, де![]() .
Функція
.
Функція ![]() на відрізку
на відрізку ![]() набуває
найменше значення в точці
набуває
найменше значення в точці![]() :
: ![]() , а найбільше значення - у єдиній
стаціонарній точці
, а найбільше значення - у єдиній
стаціонарній точці 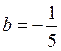 :
: 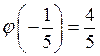 . Отже
найбільше значення функції
. Отже
найбільше значення функції ![]() в області
в області ![]() дорівнює
дорівнює ![]() , а
найменше значення дорівнює
, а
найменше значення дорівнює ![]() . Оскільки функція
. Оскільки функція ![]() неперервна в області
неперервна в області ![]() , то вона набуває всі значення від
, то вона набуває всі значення від ![]() до
до ![]() включно.
Тому величина
включно.
Тому величина ![]() (тобто
(тобто 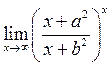 )
може набувати будь-яке значення із відрізку
)
може набувати будь-яке значення із відрізку 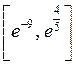 .
.
Задачі на диференціальне числення
1. З'ясувати, чи
існує дійсне число ![]() таке, що
таке, що ![]() .
.
Відповідь: не існує.
Розв΄язання.
Доведемо, що ![]() виконується нерівність:
виконується нерівність: ![]() , причому рівність має місце
, причому рівність має місце
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.