Опорний конспект з дисципліни «Вища математика» (Елементи теорії матриць і визначники. Елементи теорії границь функції однієї і багатьох змінних. Диференціальні рівняння. Числові і функціональні ряди)

Наведіть приклад диференціального рівняння 1-го порядку, яке  містить функцію .

5.  Наведіть приклад диференціального рівняння 1-го порядку, яке  містить функцію .

6.  Сформулюйте задачу Коши для диференціального рівняння 1-го порядку.

7.  Що називається загальним розв’язком диференціального рівняння 1-го порядку.

8.  Що називається розв’язком диференціального рівняння?

9.  Який вигляд має диференціальне рівняння 1-го порядку з відокремленими змінними?

10.  Який вигляд має лінійне диференціальне рівняння 1-го порядку?

11.  Який вигляд має однорідне диференціальне рівняння 1-го порядку?

12.  Метод розв’язання диференціального рівняння 1-го порядку з відокремленими змінними.

13.  Метод розв’язання лінійного диференціального рівняння 1-го порядку.

14.  Метод розв’язання однорідного диференціального рівняння 1-го порядку.

15.  Який вигляд має ЛОР 2-го порядку?

16.  Який вигляд має загальний розв’язок ЛОР 2-го порядку?

17.  Який вигляд має ЛНР 2-го порядку?

18.   Який вигляд має загальний розв’язок ЛНР 2-го порядку?

19.  Який вигляд має загальний розв’язок ЛОР 2-го порядку з постійними коефіцієнтами у випадку додатного дискримінанта  характеристичного рівняння.

20.  Який вигляд має загальний розв’язок ЛОР 2-го порядку з постійними коефіцієнтами у випадку нульового дискримінанта  характеристичного рівняння.

21.  Який вигляд має загальний розв’язок ЛОР 2-го порядку з постійними коефіцієнтами у випадку від’ємного дискримінанта  характеристичного рівняння.

22.  Серед наведених диференціальних рівнянь вказати диференціальні рівняння 1-го порядку з відокремленими змінними:

;                  ;                 .

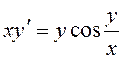23.  Серед наведених диференціальних рівнянь вказати лінійне диференціальне рівняння 1-го порядку:

;              ;                   .

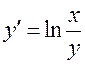24.  Серед наведених диференціальних рівнянь вказати лінійне диференціальне рівняння 1-го порядку:

;                  ;                 .

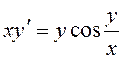25.  Серед наведених диференціальних рівнянь вказати однорідне диференціальне рівняння 1-го порядку:

;          ;            .

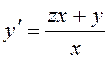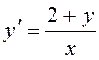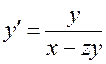26.  Серед наведених диференціальних рівнянь вказати однорідне диференціальне рівняння 1-го порядку:

;              ;                   .

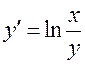27.  Метод розв’язаних ЛОР 2-го порядку з постійними коефіцієнтами.

28.  До якого типу належить диференціальне рівняння ?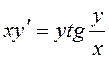

29.  До якого типу належить диференціальне рівняння ?

30.  До якого типу належить диференціальне рівняння ?

31.  До якого типу належить диференціальне рівняння ?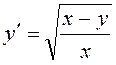

32.  До якого типу належить диференціальне рівняння ?

Розділ. ЧИСЛОВІ І ФУНКЦІОНАЛЬНІ РЯДИ

Тема. Числові ряди та їх збіжність

Поняття числового ряду та його суми. Необхідна умова збіжності числового ряду. Еталонні ряди: ряд геометричної прогресії і гармонійний ряд. Ознаки порівняння і Даламбера збіжності числового ряду з додатними членами. Знакопочерговий ряд (ряд Лейбніца) та умови його збіжності. Абсолютна та умовна збіжність знакозмінного ряду.

Тема. Функціональні ряди

Поняття функціонального ряду та області його збіжності. Рівномірна збіжність функціонального ряду та ознака Вейєрштрасса. Поняття степеневого ряду. Теорема Абеля і радіус збіжності степеневого ряду. Ряди Тейлора і Маклорена.

Розвинення функцій  у степеневі ряди. Формули Ейлера. Розвинення функцій  у степеневі ряди. Застосування степеневих рядів. Поняття ряду Фур’є.

Література:

[1], т. І, с.335-358.

[2], с.362-412.

[3], с. 379-410.

Нехай дана нескінченна послідовність чисел , , . . . , . . .. Складений з цих чисел символ

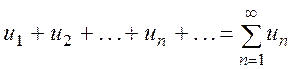, називається числовим рядом, а числа , , . . . , . . . - членами цього ряду.

Довільний член ряду  називається загальним членом. Сам по собі символ реального сенсу не має, бо вимагає визначення самого поняття суми нескінченного ряду чисел.

Сума n перших членів ряду

називається n-ою частинною сумою ряду.

Розглянемо послідовність частинних сум ряду

;

;

. . . . . . . . . . . . . . . . . .

;

. . . . . . . . . . . . . . . . . .

Означення. Якщо існує границя послідовності часткових сум ряду, то ця границя називається сумою ряду, а ряд збіжним і пишуть

.

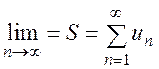Якщо ж границя послідовності часткових сум ряду не існує, то ряд називається розбіжним.

n-м лишковим членом  ряду називають різницю між сумою ряду та його n-ой частинною сумою, тобто

.

1. Якщо до ряду приписати або відкинути кілька перших членів, то характер збіжності ряду не зміниться.

2. Якщо кожний член ряду помножити на одне й те ж число, то характер збіжності ряду не зміниться.

3. Збіжні ряди

,

можна почленно додавати і віднімати, так що ряд

,                        (5)

збігатиметься, а його сума відповідно дорівнюватиме .

Необхідна ознака збіжності рядів.

Якщо ряд 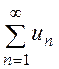   (6)

збігається, то границя його загального члена дорівнює нулю, тобто

.

Наслідок. Якщо границя загального члена відрізняється від нуля або не існує