Математика \ Численные методы

Нахождение действительных корней нелинейных и трансцендентных уравнений. Численное решение дифференциального уравнения, страница 4

где

Таким образом, метод  Рунге-Кутта  требует  на  каждом  шаге   четырехкратного  вычисления   правой  части  уравнения  f (х,у).

          Метод  Эйлера  и  его  модифицированный  вариант  также  могут  рассматриваться   как  методы  Рунге- Кутта  первого  и  второго  порядков. Метод  Рунге -Кутта  требует  большего  объема  вычислений, однако  это  окупается    повышенной  точностью, что  дает  возможность  проводить  счет  с  большим  шагом.  Другими  словами,  для  получения  результатов  с одинаковой  точностью  в  методе  Эйлера  потребуется  значительно  меньший  шаг, чем  в  методе  Рунге – Кутта.

Для  повышения  точности  численного  решения  без  существенного  увеличения  машинного  времени  используется  метод   Рунге. Он  состоит  в  том, что  проводятся  повторные  расчеты  по  одной  разностной  схеме  с  различными  шагами. Уточненное  решение  с  совпадающих  при  разных  расчетах  узлах строится  с  помощью  проведения  серии  расчетов.

Предположим, что  проведены  две  серии  расчетов  по  схеме  порядка  k  соответственно с  шагами   h и  h /2 .  В результате  расчетов  получены множествазначений   сеточной  функции yh  и yh/2. Тогда в соответствии с методом  Рунге уточненное  значение  y*h  сеточной  функции  в  узлах  сетки  с шагом  h  вычисляется  по  формуле:

Порядок  точности  этого  решения   равен  k + 1 , хотя  используемая  разностная  схема  имеет  порядок  точности  k.  Таким  образом, решение  задачи на  двух  сетках   позволяет  на  порядок  повысить  точность  результатов.

2.2 Алгоритм решения уравнения.

1.Задаём исходные значения и вводим заданную функцию.

2.Производим вычисления с помощью формул метода четвёртого порядка:

3.Если значения и меньше или равно n , то  цикл расчетов повторяется.

4.Если же условия i ≤ n не выполняется, то действия прекращаются.

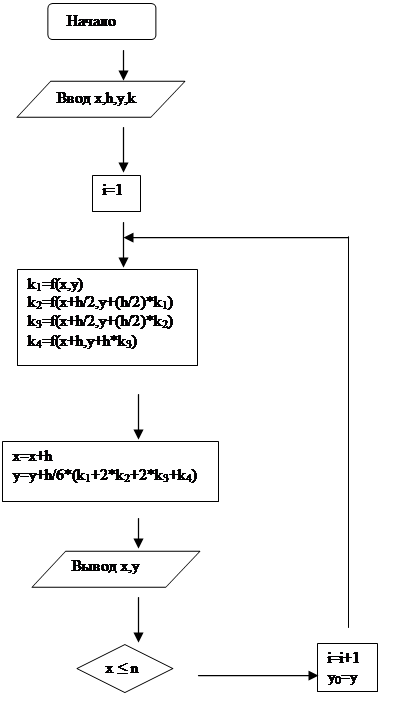
2.3.Блок-схема алгоритма


Блок-схема: альтернативный процесс: Конец


Рис.2.3. Блок-схема алгоритма метода Рунге-Кутта.

2.4.Текст программы:

program lab2;

uses crt ;

var x,y,y0,k1,k2,k3,k4,a,h,b:real;

function f(x,y:real):real;

begin

f:=cos(y)+2*x;

end;

begin

writeln('a=');read(a);

writeln('b=');read(b);

writeln('h=');read(h);

writeln('y0=');read(y0);

x:=a;

y:=y0;

writeln('x=',x:7:5,'y=',y:7:5);

repeat

k1:=f(x,y);

k2:=f(x+(h/2),y+(h/2)*k1);

k3:=f(x+h/2,y+h/2*k2);

k4:=f(x+h,y+h*k3);

x:=x+h;

y:=y+h/6*(k1+2*k2+2*k3+k4);

writeln('x=',x:7:5,'y=',y:7:5);

until x>b;

readkey;

end.

2.5. Результаты решения.

В ходе вычисления методом Рунге-Кутта был получен  результат численного решения дифференциального уравнения f(x,y)=cosy+2x, при начальном условии у(1)=1, заданном интервале 1…2  и шаге 0.1 приведенный в таблице (2.5.1).

Таблица 2.5.1.Результаты вычисления

X

Y

1.00000

1.00000

1.10000

1.25285

1.20000

1.50199

1.30000

1.74661

1.40000

1.98747

1.50000

2.22650

1.60000

2.46666

1.70000

2.71177

1.80000

2.96660

1.90000

3.23699

2.00000

3.53020

2.6.График функции.

 


Рис.2.6.1. График функции f(x,y)=cosy+2x

3.СПИСОК  ЛИТЕРАТУРЫ.

1. Бахвалов Н.С.  Численные  методы. - М.: Наука, 1988. - 274 с.

2. Волков Е.А.    Численные  методы. - М.6 Наука,  1990. -  316 с.

3. Самарский А.А. Введение  в численные  методы – М.: Наука, 1989. - 336 с.

 4. Щуп Т.  Решение инженерных  задач  на  ЭВМ. - М. 6 Мир, 1989. -             221 с.

  5. Корн Г.,  Корн Т. Справочник  для  научных  работников и  инженеров. -                             М. : Наука, 1984, - 732 с.

6. Бронштейн И.Н., Симендяев К.А. Справочник  по  математике  для  инженеров  и  учащихся  втузов. - 13-е мзд.,  испр. - М. :  Наука,  1986. - 544 с.

7.Турчак Л.И.  Основы численных методов. – 1987г.

Скачать файл