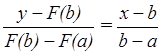Нахождение действительных корней нелинейных и трансцендентных уравнений. Численное решение дифференциального уравнения, страница 2

,          (1.1.2)

Для  точки  пересечения  ее с  осью  абсцисс (х  =x* ,  у  =  0 )  получим  уравнение 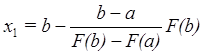                                                                                                                                                                                                                                                                                                                       (1.1.3)

Далее, сравнивая  знаки  величин   F (b)  и  F ( x*)  для  рассматриваемого  случая, приходим  к  выводу, что  корень  находится  в  интервале  (а, x*), так  как  F (b)· F (x*)< 0. Oтрезок  [x*,a]  отбрасываем.  Следующая  итерация  состоит  в определении  нового  приближения  с     как  точки  пересечения  хорды   АВ   с  осью  абсцисс  и  т.д.  Итерационный  процесс  продолжается  до  тех  пор , пока  значение  F (x_k)  не  станет  по  модулю  меньше  заданного  числа   e.

…………………………………………..

Алгоритмы  метода  деления отрезка  пополам  и  метода  хорд  похожи, однако  второй  из  них  в  ряде  случаев  дает  более  быструю сходимость    итерационного  процесса.  При  этом  успех  его  применения ,  как  и  в  методе  деления отрезка  пополам, гарантирован.

1.2. Отделение  корней

Для  отделения  корней  необходима  следующая  теорема.

Если непрерывная  функция  на  разных  концах  конечного  интервала принимает значения разных знаков, то внутри этого интервала содержится,  по  крайней  мере, один  корень.

       Таким  образом,  процесс отделения  корней  начинается  с  установления  интервалов, на  границах  которых  функция  принимает  значение  разных  знаков.  На практике этот  процесс обычно  выполняют   графическим  способом.  Его  сущность заключается  в  следующем.

        Исходная  функция  произвольно разбивается   на  две  функции. Затем  в одних  координатных  осях  строятся  графики  этих  функций. Количество  точек пересечения  равно числу  корней  исходного  уравнения, а абсциссы  точек  пересечения  соответствуют  значениям  корней  исходного  уравнения.

y=e^x - 2x² + 1.5

x	Y
-2	6.5
-1.5	3
-1	0.5
0	-1.5
1	0.5
1.5	3
2	6.5

x	y
-∞	-∞
-2	0.14
-1	0.37
0	1
1	2.72
2	7.389
+∞	+∞

e^x=2x² – 1.5

 

Рис.1.2.1. Отделение  корней графическим способом.            

1.3 Алгоритм решения уравнения

1.Определяем значения функций на границах интервала.

2.Находим величину x₁ и f(x₁).

3.Если знак функции в полученной точке совпадает со знаком в левой границе интервала, то получаем новый интервал для вычисления последующего.

4.Вычисления заканчиваются тогда, когда абсолютная разность по модулю между последующим и предыдущим значением становится меньшей наперед заданного числа ε. (|χ_к+1-χ_с|≤ ε)

5.После достижения заданной (нужной) точности, определяем погрешность найденного решения.

1.4.Блок-схема алгоритма

Блок – схема  метода  хорд   приведена  на  рис. 1.4.1.   В блок-схему  необходимо  ввести операторы  вычислений  значений   F ( х )  на  границах  новых  отрезков.

Алгоритмы  метода  деления отрезка  пополам  и  метода  хорд  похожи, однако  второй  из  них  в  ряде  случаев  дает  более  быструю сходимость    итерационного  процесса.  При  этом  успех  его  применения ,  как  и  в  методе  деления отрезка  пополам, гарантирован.

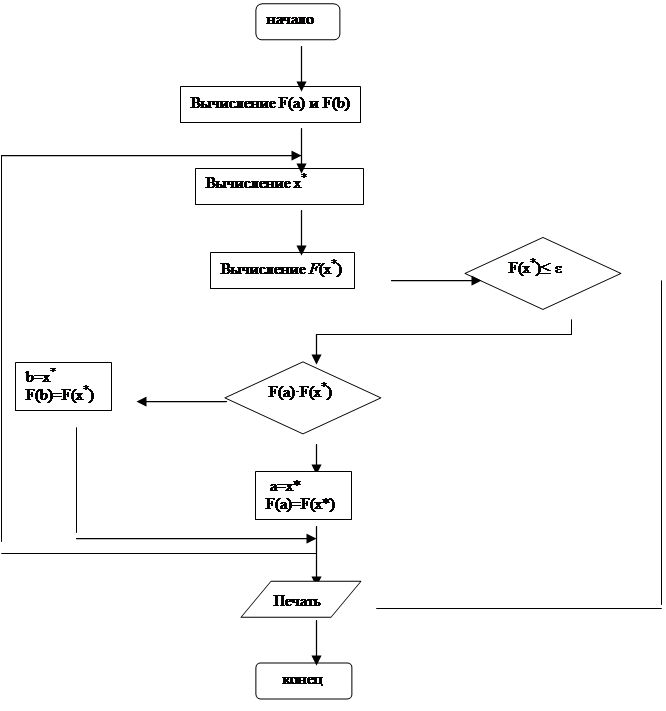Рис.1.4.1. Блок-схема метода ХОРД

1.5.Текст программы

Program lab1;

uses crt;

var x,y,a,b,eps,xn:real;

function f(x:real):real;

begin

f:=exp(x)-2*sqr(x)+1.5;

end;

function f2(x:real):real;

begin

f2:=exp(x)-4;

end;

begin

writeln ('a=');read (a);

writeln ('b=');read (b);

writeln ('eps=');read (eps);