Исследование точности и стабильности технологического процесса обработки кольца подшипника

5. ИССЛЕДОВАНИЕ ТОЧНОСТИ И СТАБИЛЬНОСТИ ТЕХНОЛОГИЧЕСКОГО ПРОЦЕССА ОБРАБОТКИ КОЛЬЦА ПОДШИПНИКА

Объектом исследования технологии механообрабатывающего производства является поверхность детали, формируемая определенной технологической системой. Технолога, прежде всего, интересуют такие показатели объекта, как точность  поверхности и ее качество.

Точность определяется допуском на размер или на отклонение от формы и расположения поверхностей. Допуск на размер является допустимой погрешностью обработки и объединяет в себе все виды сопровождающих обработку погрешностей: постоянной или систематической, функциональной или закономерно изменяющейся во времени и случайной. Поэтому исследование точности технологического процесса предполагает необходимость установить наличие и количественно оценить все виды погрешностей. Имея такую информацию, технолог  может грамотно, обоснованно принимать решения ля эффективного управления технологическим процессом.

Носителем обобщенной информации о точности технологического процесса, о вкладе каждого из элементов технологической системы в итоговую погрешность, о доли каждого вида погрешностей в ней является размер детали. Поэтому, определенным образом собирая и исследуя информацию о размере детали можно выделить  и количественно определить все виды погрешностей.

Методика исследования размера детали для выявления всех видов погрешности основана на исследовании размера как случайной величины. Случайный характер размера отражает его природу, которая состоит в том, что колебание размеров деталей на налаженном станке вызывается множеством причин, устранить которые полностью невозможно. Влияние их можно только уменьшить до какого-то определенного уровня.

5.1 Обработка и анализ результатов наблюдения за случайной величиной, представленной интервальным рядом

Если выборка из генеральной совокупности велика (объём выборки N более 50), то ее удобно представлять интервальным рядом. Для этого весь диапазон исследуемого признака x разбивают на K-интервалов с равномерным шагом h. Каждому значению признака, попавшему в i-тый интервал, присваивают значение середины интервала – x_i. В результате получают не N значений исследуемого признака, а только К.

Число значений исследуемого признака, попавших в i-тый интервал, называют частотой интервала n_i.

Скуппированные таким образом результаты наблюдений в виде перечня значений середин интервалов x_i, расположенных в возрастающем порядке с соответствующими им частотами n_i, и есть интервальный ряд.

Цель анализа интервального ряда состоит в подборе теоретического распределения, хорошо описывающего экспериментальное, статистическое, т.е. интервальный ряд.

Для выбора гипотетического, предлагаемого, теоретического распределения необходимо построить гистограмму статистического распределения и по ее виду можно выбирать предполагаемое теоретическое распределение.

Проверка соответствия предполагаемого теоретического распределения результатам наблюдения, т.е. статистическому распределению, производится сначала расчетом теоретических частот nt_i, с использованием дифференциальной функции (плотности) теоретического распределения, сравнением их с эксперементальными n_i.

Визуальное сравнение графиков n_i(x_i), nt_i(x_i) позволяет более строго оценить возможность применения выбранного теоретического распределения для описания статистического.

Однако и такая оценка является субъективной. Поэтому окончательный вывод о соответствии теоретического распределения статистическому производится по критериям согласия.

Наибольшее распределения для такой проверки получили критерии Колмогорова и Пирсона.

Критерий Колмогорова λ вычисляется следующим образом:

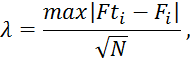
где Ft_i – интегральная функция теоретического распределения для значения x_i; F_i – интегральная функция статистического распределения для значения x_i.

Если значение λбудет меньше табличного значения критерия Колмогорова λ_1-р, где р - уровень значимости, то гипотеза о соответствии теоретического распределения статистическому подтверждается, принимается. Иначе она отклоняется. Табличное значение λ_1-р выбирается из таблицы квантилей распределения Колмогорова[ ].

Уровень значимости Р для критерия Колмогорова выбирается жестким, равным 0,2 или даже 0,3.

Пример анализа интервального ряда

Все расчеты при анализе и построение графиков удобно выполнять в пакете «Mathcad», что и иллюстрируется нижеприведенным примером. Распечатка всех расчетов на с приложении А.