Исходные данные для интервального ряда – в левом верхнем углу приложения А. Значение середины интервалов xi задано дискретным аргументом. Число интервалов – 8, размер интервала h-0,2. Значение частот интервалов ni заданы в виде столбца с перечислением частот через запятую.
Правее столбца с ni приведена гистограмма статистического распределения. В «Mathcad» - это одномерный график , где по оси абсцисс (по оси Х) отложены значения xi а по оси ординат (оси Y) – значения ni в виде прямоугольников (bar) что задается в меню одномерного графика.
По виду гистограммы, которая, которая напоминает колокообразную кривую плотности нормального распределения, можно высказать гипотезу о приемлемости нормального распределения для описания наблюдаемого, статистического распределения.
Чтобы вычислить теоретические частоты nti и затем сравнить их с эмпирическими ni, нужно рассчитать оценки числовых характеристик предполагаемого нормального распределения.
Правее столбца с ni приведен расчет объема выборки N среднего арифметического xi как оценки математического ожидания a, и выборочного среднего квадратического отклонения S, как оценки теоретического среднего квадратического отклонения σ.
Подставив значения xc и S вместо α и σ в формулу плотности нормального распределения, получим формулу для ее расчета:
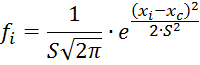
Теоретические частоты nti вычисляются по формуле:
![]()
В нашем примере размер интервала h=0,2.
В середине приложения А приведены рядом столбцы значений nti и ni для их сравнения, а правее – графики ni(xi) и nti(xi).
Сравнение графиков наглядно показывает, что теоретическое распределение (пунктирная линия) с большой погрешностью описывает статистическое.
Окончательный вывод о приемлемости нормального распределения выполняем по критерию Колмогорова.
Значения функций распределения теоретического Fti и эмпирического Fi для i-го значения исследуемого признака вычисляем по формулам:
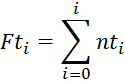
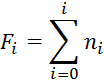
Затем вычисляем λ и сравниваем его с λ1-р, где Р=0,2.
Из приложения А видно, что λ=1,07. Так как λ>λ0,8, то следует сделать вывод – нормальное распределение плохо описывает статистическое, наблюдаемое.
5.2. Исследование точности и стабильности технологического процесса обработка деталей методом большой выборки
Теоретические положения
Методом большой выборки исследуются технологические процессы полностью устойчивые, т.е. те, у которых математическое ожидание и дисперсия исследуемого признака неизменны во времени. Большая выборка – выборка объемом N≥50. Взяв выборку из 50 или более деталей, последовательно обработанных на какой-то операции механической обработки на налаженном оборудовании, производят статистический анализ относительно размера, формируемого на этой операции.
Рассмотрим основные этапы исследования.
1.Формируется интервальный ряд (xi, ni);
2.Вычисляются основные характеристики хa и S (среднее арифметическое и выборочное среднее квадратическое отклонение соответственно):
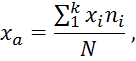
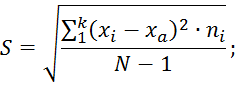
3.Вычисляются теоретическое (выравнивающие) частоты ni и теоретические nti построением гистограммы частот ni(xi) и зависисости
nti(xi) на одном графике;
4.Производится проверка нулевой гипотезы, т.е. гипотезы о соответствии предпологаемого нормального распределения наблюдаемому (статистическому) по критериям согласия Колмогорова и Пирсона.
Критерий Колмогорова вычисляется следующим образом :
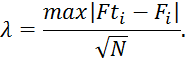
Расчетное
значение критерия Колмогорова ![]() сравнивается с λ1-р,
взятым из таблиц квантилей распределения Колмогорова (приложение 4 [ ]), где Р –
уровень значимости. Уровень значимости рекомендуется Р=0,2..0,3. Если
сравнивается с λ1-р,
взятым из таблиц квантилей распределения Колмогорова (приложение 4 [ ]), где Р –
уровень значимости. Уровень значимости рекомендуется Р=0,2..0,3. Если ![]() λ1-р, то нулевая
гипотеза принимается.
λ1-р, то нулевая
гипотеза принимается.
Расчетное значение критерия Пирсона:
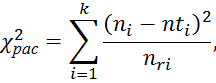
где
К – число интервалов. ![]() 2
сравнивается с квантилями распределения Пирсона
2
сравнивается с квантилями распределения Пирсона ![]() (Приложение 5 []), которые
определяются в зависимости от Р – уровня значимости и числа степеней свободы f=
К-3.
Если
(Приложение 5 []), которые
определяются в зависимости от Р – уровня значимости и числа степеней свободы f=
К-3.
Если ![]() , то нулевая гипотеза принимается.
, то нулевая гипотеза принимается.
Для критерия Пирсона имеется ограничение на теоретическую частоту интервала nti. Она должна быть не менее 5. Если это не соблюдается, то интервал с nti<5 объединяется с соседним.
Если нулевая гипотеза принимается, то следует важный вывод – технологический прочес полностью устойчивый (стабильный).
После
этого производится сравнение результатов наблюдения с требованиями чертежа.
Допуск δ на размер по чертежу и достоверный диапазон рассеивания наблюдаемого
размера - 6![]() S
сравниваются вычислением коэффициента точности Km:
S
сравниваются вычислением коэффициента точности Km:
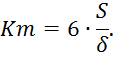
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.